RAPP: NOVELTY DETECTION WITH RECONSTRUCTION ALONG PROJECTION PATHWAY 정리글
Abstract
autoencoder를 활용하여 anomaly detection을 수행하는 시도들이 있다. 하지만, 이러한 방법론은 주로 input과 reconstruct된 output간의 차이에 집중하고, hidden space간의 관계에 대해서는 고려하지 않는다는 한계를 가지고 있다. 본 연구에서는 autoencoder 구조를 바탕으로 input space와 output간의 관계뿐만 아니라, hidden space간의 관계를 고려하는 방법을 제안한다. (encoder hidden space와 대응되는 decoder hidden space와 비교) 또한, reconstructed된 output을 다시 동일한 autoencoder에 넣어서 발생되는 activation value가 original input을 동일한 모델에 넣었을때의 대응되는 decoder activation value와 동일하다는 것을 보였다.
Introduction
아쉽게도 encoder hidden space와 대응되는 decoder hidden space를 비교하는 것은 불가능하다. 왜냐하면, 학습이 진행되는 동안은 모델이 불안정하며 encoder-decoder layer pair가 대응된다고 볼 수 없기 때문이다. 하지만 reconstructed된 output을 다시 동일한 autoencoder에 넣어서 발생되는 activation value가 original input을 동일한 모델에 넣었을때의 대응되는 decoder activation value와 동일하다는 것을 보임으로써 문제를 해결할 수 있었다.
Contributions
- hidden space도 함께 활용한 방법론
- RaPP의 motivation 소개 및 증명
- RaPP의 성능 증명
Proposed Method RaPP
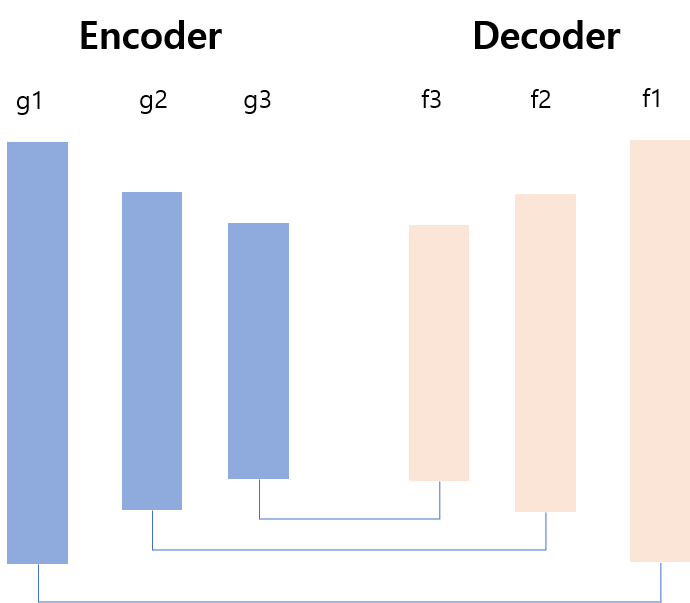
위의 이미지 처럼 encoder와 decoder간의 hidden space를 비교하는 것이 목표이지만, 위에서 언급한 한계때문에 불가능하다. 그래서 새롭게 제안하는 방법은 reconstruction output을 다시 autoencoder에 넣어서 decoder의 hidden space들을 재현하는 것이다.
Reconstruction Based Novelty Detection
autoencoder $A$ 는 unsupervised 방법을 바탕으로 의미있는 representation을 만들어내며, 아래는 사용되는 objective이다. 또한, $\epsilon(x)$가 높다면, anomaly일 가능성이 높아진다고 해석할 수 있다. 하지만, 모델의 구조가 깊어질수록 hierarchical information을 활용하지 못하는 점에서 아쉬움이 남는다. 딥러닝 모델의 모든 layer를 충분히 활용하려면 결국 hidden space를 잘 활용할 필요가 있다.
Reconstruction Error In Hidden Spaces
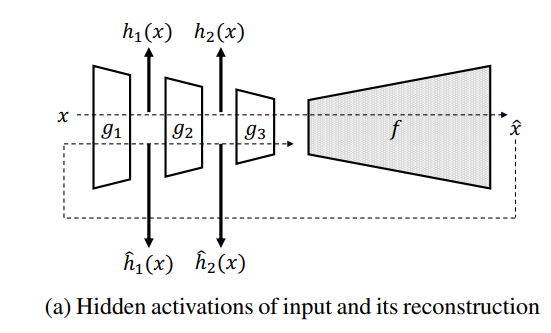
위에 보이는 이미지처럼, $h_i(x), \hat{h}_i(x)$를 각각 구한다.
다음과 같은 encoder를 정의하면 위의 과정을 전개할 수 있다.
그리고 위와 같은 hidden space value들을 decoder hidden space의 수 만큼 모아준다. $H(x)$를 활용해서 novelty score를 얻기 위해 다음과 같은 과정을 진행한다.

여기서 $S$ 는 novelty score를 측정하는 함수로 본 연구에서는 크게 두 가지 방향을 제시한다.
Simple Aggregation Along Pathway(SAP)
두 hidden space간의 Euclidean distance를 구한다.
Normalized Aggregation Along Pathway(NAP)
위의 SAP 방법은 각 hidden space간의 특성은 고려하지 못한다. 각 pair마다 distance distribution이 다르게 나타날 수 있는데 이러한 문제를 해결하기 위해서 orthogonalization과 scaling을 통한 normalization 방법을 제안한다.
- $d(x) = h(x) - \hat{h}(x)$
- $D$ 는 matrix이며 각 row i는 data point $x_i$가 가지고 있는 pair들의 distance들로 이루어져있다.
- $\bar{D} $는 $D$의 column wise centered matrix 이다.
- normalization을 위해서 SVD를 수행한다. $\bar{D} = U \Sigma V^T$
Motivation Of RAPP
‘hidden space정보를 활용할 수 있지 않을까’라는 동기에서 연구가 출발했다. 하지만, 이런 문제의식을 가지더라도 해결해야될 이슈가 있다. 대응하는 encoder decoder의 layer pair가 서로 같은 space를 표현한다고 할 수 없다. 왜냐하면, autoencoder의 objective는 각 layer에 들어오는 input에 대해서 어떤 제약도 하지 않기 때문이다. 결과적으로 $f_{l:i+1}(g(x)) = g_{:i}(x)$과 같은 관계가 성립한다고 볼 수 없다.
그럼에도 불구하고, $\hat{h}i(x) = g(A(x))$의 관계를 바탕으로, 위의 문제의식을 실현할 수 있었다. 전반적인 프로세스는 아래의 Figure1 (b)를 확인하면 알 수 있다.
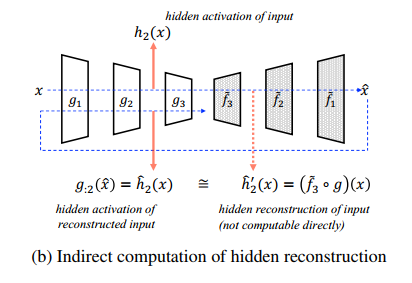
Computation Of Hidden Reconstruction
- $A = f \circ g$은 학습된 autoencoder라고 가정한다.
- $M_0 = { A(x): x \in R^n }$은 reconstruction된 output 집합이다.
- $A$는 다음과 같이 표현된다. $ x\in M_0, x= A(x)$
- 해석하자면, reconstruction된 결과를 다시 autoencoder에 넣으면 input으로 넣은 reconstruction과 동일하다는 것이다.
- $M_i = { g_{:i(x)}: x \in M_0 }$
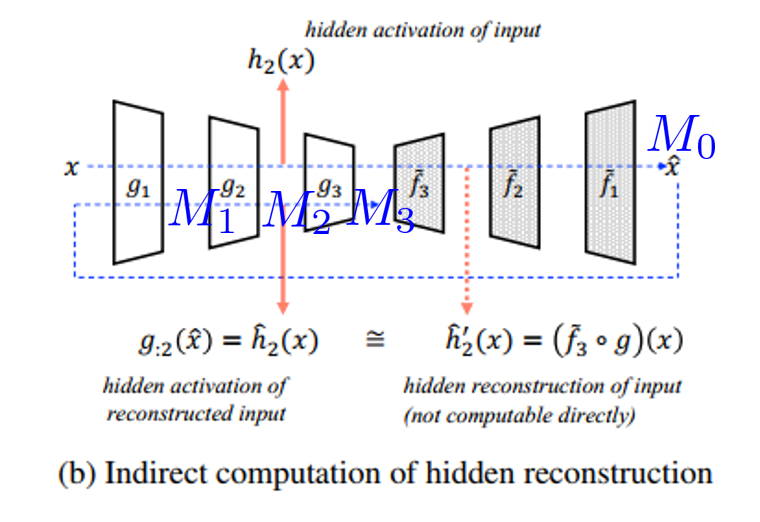
다음과 같은 decoder $\tilde{f}$ 가 있다고 가정하자.
첫 번째 조건 $x \in M_l, \tilde{f}(x) = f(x)\ $은 feed foward의 결과가 같다는 것을 의미한다.
두 번째 조건$a \in M_i, a = (g_i \circ \tilde{f})(a)$은 $\tilde{f}{l:i+1}$과 $g{i+1:}$이 서로 적합한 encoder decoder의 pair로 만들어준다. 즉 서로 inverse의 관계를 가진다. 따라서 다음과 같은 수식 전개가 가능하다. 이는 Figure1 (b)를 보면, 어떤 의미인지 알 수 있다. 간략히 설명하면, decoder 부분의 hidden space다.
그리고 다음과 같은 과정을 통해서 $\hat{h^{‘}}_i(x) = \hat{h}_i(x)$임을 증명할 수 있다.
주목할 점은 $\hat{h^{‘}}_i$을 얻기 뒤해서 $\tilde{f}_i$가 필요하지 않다는 것이다. 그리고 $x \in M_0$에 대해서는 다음과 같은 관계도 성립한다.
Existence of f_tilde
전제조건은 다음과 같다.
- $x = A(x) \text{ for } x \in M_0$
- $g_i(x: x \in M_{i-1}) = \hat{x}: \hat{x} \in M_i$
- $f_i(x: x \in M_{i-1}) = \hat{x}: \hat{x} \in M_i$
여기에 다음과 같이 정의해보자.
$\tilde{f}_i =g_i^{-1} \text{ for } M_i$이라면, 이런관계가 성립한다. $\tilde{f} = g^{-1}$ 해석하면, 각 encoder decoder layer pair에 대해서 inverse 관계가 성립하게 되면, encoder decoder에 대해서도 inverse 관계가 성립하게 된다.
이런 정의는 아래와 같은 조건을 충족시킨다.
$x = A(x)$ 라는 전제조건을 생각해보면,
Existence of f_tilde With Neural Networks
neural network는 유연한 구조를 가졌기때문에, 특정 함수를 쉽게 근사할 수 있다.