Sorting Algorithm
Content
- Insert sort
- Merge sort
- Quick sort
- Heap sort
Insert Sort
insert sort는 일반적으로 적은 수의 요소들을 정렬할 때 유리하다.
insert sort는 배열이 주어졌을 때, 순차적으로 순회하면서 각 요소의 올바른 위치로 정렬한다. 만약, i 번째까지 순회하였다면, 0 ~ i번째의 배열은 0 ~ i번째 배열의 성분 기준으로 모두 알맞은 위치에 정렬된 상태이다. i + 1번째 요소는 알맞게 정렬된 0 ~ i번째 배열기준으로 알맞은 위치로 삽입된다.
이를 의사코드로 나타내면 다음과 같다.
for i in range(1, len(A)):
key = A[i] # 알맞은 위치로 가야하는 성분
# Insert into the sorted sequence A[:i]
j = i - 1
while j > 0 and A[j] > key:
A[j + 1] = A[j]
j -= 1
A[j + 1] = key
이해를 돕기 위해서 아래의 이미지를 첨부하였다.
Loop invariants and the correctness of insertion sort
위의 의사코드에서 i index는 현재 정렬해야 되는 성분을 의미하며, A[:i]는 0 ~ i - 1의 성분들을 의미한다. 이 때 A[:i ]는 정렬되기전의 A[:i]와 구성요소는 모두 같으면서 정렬된 배열을 의미한다. 이러한 성질을 CS에서는 loop invariants라고 한다. 그리고 이런 성질은 correcteness를 증명하는데 사용된다.
loop invariants는 3가지 조건을 충족해야한다.
- Initialization: 첫 번째 순회에서 참이어야 한다.
- Maintenance: 순회를 돌기전에 참이라면, 다음순회를 시작하기 전까지 참이어야 한다.
- Termination: 전체 순회가 끝날때, loop invariant가 해당 알고리즘이 정확하다는 것을 알려줘야 한다.
예시를 들어보겠다.
A = [0, 3, 8, 2, 1, 4]
-
Initialization
index번호가 1부터 시작한다.(A[i] = 3) 따라서 A[:i] = [0]이다. 그리고 이는 항상 참이다.\
-
Maintenance
순회를 하는 동안 i는 1, 2, 3, 4 …의 값을 가질 것이다. 정렬된 subarray A[:i]는 기존의 정렬되지 않은 A[:i]와 구성요소는 같다. (Loop invariant)
-
Termination
전체 순회가 종료되었을 때를 생각해보자. (i = len(A) - 1)
순회를 할때마다, i는 1씩 증가하게 되므로, 알고리즘이 종료될 때는 i=len(A) - 1이 된다. 이때 subarray는 A[:i] 이므로 0 ~ len(A) - 2의 범위를 가지게 된다. (정렬된 상태이다.) 그러므로 마지막 성분 A[i]만 올바른 위치에 정렬하면 된다.
Analyzing algorithms
- input size: array size
- running time: 주어진 input에 대해서 주된 연산의 call 수

- best case: O(N)/O(1)
- 모두 정렬되어 있을 경우 $c_5 \sum_{j=2}^n t_j + c_6 \sum_{j=2}^n (t_j - 1) + c_7 \sum_{j=2}^n (t_j - 1)$ 은 무시해도 좋다.
- worst case: O(N^2)/O(1)
- 모두 거꾸로 정렬되어 있을 경우
- order of growth: O(N^2)/O(1)
- 해당 알고리즘의 upper bound
Merge sort: devide-and-conquer
devide-and-conquer 방법론은 문제를 본래의 문제와 유사한 작은 문제로 나누어 해결한다.
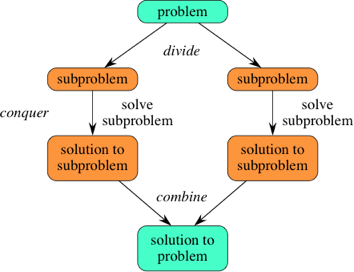
- devide: problem -> subproblem, subproblem의 성질은 기존의 problem과 동일하다.
- conquer: subproblem의 크기가 충분히 작다면, 해를 도출한다.
- combine: subproblem을 해를 고려하여 상위의 problem의 문제를 해결한다.
merge sort는 전형적인 devide-and-conquer 방법론이다.
- devide: array를 2개의 작은 array로 나눈다.
- conquer: 두개의 작은 array를 재귀적으로 정렬한다.
- combine: 두개의 정렬된 작은 array를 합치면서, 정렬된 array를 도출한다.

merge sort는 두 가지 방법으로 구현할 수 있다. 아래는 python으로 제작한 의사코드이다.
Top-Down approach: recursive
def merge(A, p, q, r):
"""
A[p:q+1]와 A[q+1:r+1]을 합친다.
A: 합쳐지기 전 array, A[p:q+1], A[q+1:r+1]은 각각 정렬된 상태
"""
arr, i = [0] * (r - p + 1), 0
while p < q and q < r:
if A[p] < A[q]:
arr[i] = A[p]
p += 1
else:
arr[i] = A[q]
q += 1
if p < q - p - 1:
arr[i+1:] = A[p:q+1]
if q < r - q - 2:
arr[i+1: ] = A[q+1:r+1]
A[p:r+1] = arr
def merge_sort(A, p, r):
'''
A: 정렬되지 않은 array
p: left index
r: right index
'''
if p < r:
q = (p + r) // 2
merge_sort(A, p, q)
merge_sort(A, q + 1, r)
merge(A, p, q, r)
Bottom-up approach: iterative
def merge(A, p, q, r):
"""
A[p:q+1]와 A[q+1:r+1]을 합친다.
A: 정렬되지 않은 array
"""
arr, i = [0] * (r - p + 1), 0
while p < q and q < r:
if A[p] < A[q]:
arr[i] = A[p]
p += 1
else:
arr[i] = A[q]
q += 1
if p < q - p - 1:
arr[i+1:] = A[p:q+1]
if q < r - q - 2:
arr[i+1: ] = A[q+1:r+1]
A[p:r+1] = arr
group_size = 1
while group_size < len(A):
i = 0
while i < len(A):
merge(A, i, i + group_size, i + 2*group_size + 1)
i += group_size * 2 + 2
group_size *= 2
Loop invariant
insert sort와 마찬가지로 loop invariant 성질을 이용하여 corrteness를 증명할 수 있다.
- Initialization: 초기에는 subarray가 비워진 상태로 시작한다.
- Maintainance: 위의 의사코드에서 알 수 있듯이 subarray의 성분의 index는 바뀌지만 전체 성분은 변하지 않는다.
- Termination: 마지막 두 개의 subarray를 합칠 때를 고려해보자. 각각의 subarray는 정렬되어 있는 상태이다. 따라서 merge 알고리즘을 그대로 적용한다면, 결과는 모두 정렬되어 나올 것이다.
Analyzing divide-and-conquer algorithms
recursive한 알고리즘을 사용했다면, running time을 recurrence equation을 활용해서 표현할 수 있다. 아래는 예시이다.
- subarray가 충분히 작다면: $\mbox{if } n > c$
- $T(n/b)$: $n/b$ subarray의 크기, $a$ 는 subarray의 개수
- $D(n)$: array를 subarray로 나누는데 걸리는 시간
- $C(n)$: combine
이제 merge sort를 분석해보자.
- divide: $D(n) = O(1)$, subarray의 중간까지만 나눈다.
- conquer: $2T(N/2)$
- combine: $C(n) = O(n)$

- time complexity: O(nlogn)
- space complexity: O(nlogn)
Quick Sort
-
worst case: O(n ^ 2)
-
expected: O(nlogn) constant factor가 다른 기법에 비해서 작은 편이다.
quick sort 역시 divide-and-conquer의 한 방법이다.
-
Divide: Array를 두개의 subarray로 나눈다. $A[p…r]$을 $A[p..q-1]$,$A[q + 1.. r]$
로 나누는 것이다. $A[p..q-1]$은 $A[q]$보다 작거나 같다. 또한 $A[q + 1.. r]$은 $A[q]$ 보다 크거나 같다. 나중에 언급하지만 $A[q]$는 pivot이다.
-
Conquer: $A[p..q-1]$,$A[q + 1.. r]$를 재귀적으로 정렬한다.
-
Combine: subarray가 모두 정렬되어 있기 때문에, 따로 결합할 필요가 없다.
quick sort의 의사코드는 아래와 같다.
def quick_sort(A, p, r):
if p < r:
q = partition(A, p, r)
quick_sort(A, p, q - 1)
quick_sort(A, q + 1, r)
def partition(A, p, r):
x = A[r] # pivot value
i = p - 1
for j in range(p, r-1):
if A[j] <= x: # pivot보다 왼쪽에 위치해야한다.
i += 1
A[i], A[j] = A[j], A[i]
A[i+1], A[r] = A[r], A[i + 1]
return i + 1
partition이 이해가 안되다면 아래의 그림을 참고해보면 좋다. 참고로 i index는 pivot보다 작거나 같은 값을 가졌다는 것을 알려주며, j index는 탐색하는 의도로 구성되었다.
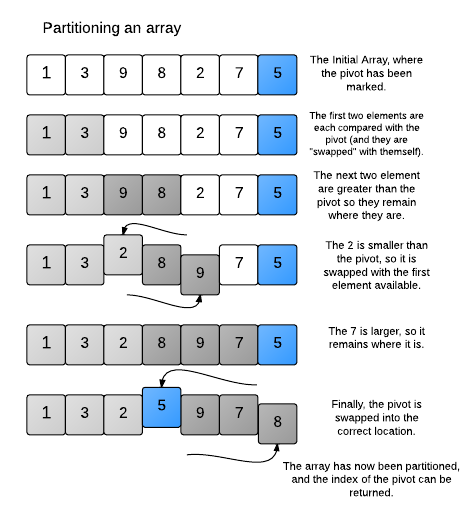
Loop invariant
-
Initialization
i = p - 1 이고 j = p 이다. p와 i 사이에는 value가 없다. 그리고 i + 1과 j- 1사이에도 아무것도 없다. 따라서 loop invariant 조건을 충족한다. (swap이 일어나지 않는다.)
-
Maintainance
위의 그림에서 볼 수 있듯이, pivot value에 따라서 성분의 배치가 달라질 수 있다. 하지만, 배치만 달라질뿐 전체 성분은 변하지 않는다.
-
Termination
알고리즘이 종료될 때는 3가지 set이 주어진다. pivot보다 작은 set, pivot, pivot보다 큰 set 이렇게 주어지게 되는데, 이는 내부적으로 모두 정렬된 상태이다.
Performance of quicksort
-
worst-case
partitioning이 1: n-1식으로 계속해서 나눠지면 최악의 성능 O(N^2)이다.
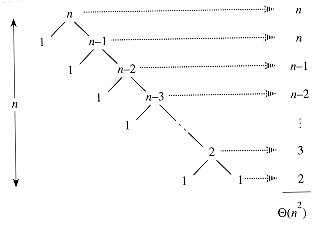
-
balanced partioning
partitioning이 모두 고루게 나눠지면 성능은 O(NlogN)이다.