Mixture density Network: Uncertainty estimation

• Problem
• Mixture Density Network
• Uncertainty Estimation Method
  • uncertainty Acquisition in Deep Learning
  • PROPOSED UNCERTAINTY ESTIMATION METHOD

Problem

기존의 방법론들은 uncetrainty를 estimate하는데 sampling을 해야하는 한계가 있다. 이 논문에서는 gaussian mixure model을 활용한 sampling-free uncertainty estimation방법론을 제안한다.

Mixture Density Network

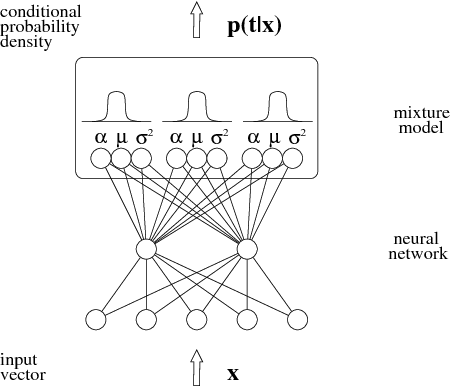
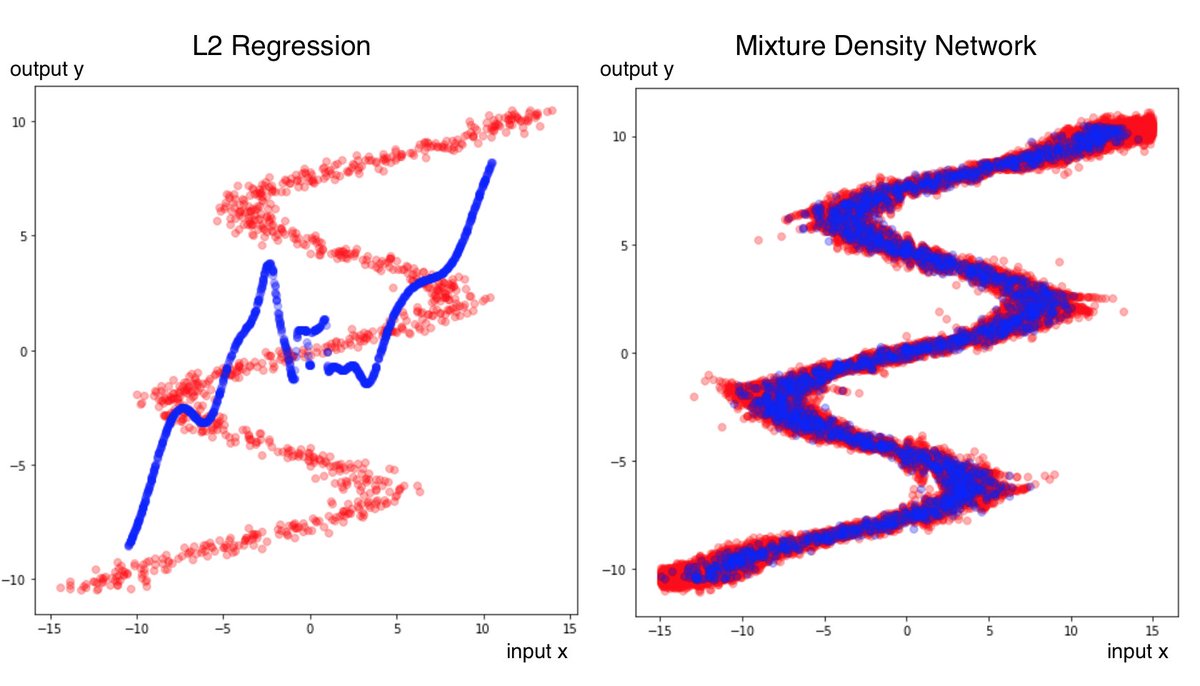
위의 이미지처럼 MDN은 output이 fixed value가 아닌 distribution의 형태를 가진다. 이런 특성 때문에 multi modal한 상황에서도 학습이 잘 진행된다.

MDN을 수식으로 나타내면 아래와 같다.

$$p(y \mid \theta) = \sum_{j=1}^K\pi_j\mathcal{N}(y \mid u_j, \Sigma_j)$$

where

• $\theta={\pi_j, u_j ,\Sigma_j }_{j=1}^K$

• $\pi_j$ : 가중치, 0 ~ 1사이의 값, $\sum_{j=1}^K\pi_j = 1$

$$\pi_j=\frac{\exp(\hat{\pi_j}-\max(\pi))}{\sum_{k=1}^K\exp(\hat{\pi_k}-\max{\pi})}$$ $$u_j=\hat{u}_j$$ $$\Sigma_j=\sigma_{\max}diag(p(\hat{\Sigma_j}))$$ $$p(x) = \frac{1}{1 + \exp(-x)}$$

$\pi_j$를 구할 때 max값을 빼주는 이유는 exponential 연산이 불안정하기 때문이다. 마찬가지로 $\sigma_{\max}$를 곱해주는 것도 possitive constant로 만들어주기 위함이다.

MDN의 loss function은 아래와 같이 구성된다.

$$c(\theta;D) = -\frac{1}{N}\sum_{i=1}^N\log(\sum_{j=1}^K\pi_j(x_j)\mathcal{N}(y_i \mid u_j(x_j), \Sigma_j(x_j)+\epsilon)))$$

Uncertainty Estimation Method

uncertainty Acquisition in Deep Learning

일반적인 딥러닝 모델을 아래와 같이 수식으로 전개한다.

$$y=f(x) + \epsilon$$

$f(x)$는 target function을 의미하고, $\epsilon$은 measurement error를 의미한다.

만약 우리가 $\hat{f}(x)$를 학습시킨다고 가정하면, 아래와 같이 분산식을 구할 수 있다.(epistemic)

$$\sigma_e^2 =E\rVert f(x) - \hat{f}(x) \rVert^2$$

위의 수식은 다음과 같이 전개된다.

$$\begin{align} E\rVert y - \hat{f}(x) \rVert^2 &=E\rVert y -f(x) +f(x)- \hat{f}(x) \rVert^2\\ &=E\rVert y - f(x) \rVert^2 + E\rVert f(x) - \hat{f}(x) \rVert^2 \\ &=\sigma_a^2 + \sigma_e^2 \end{align}$$

여기서 $\sigma_a^2$은 aleatoric uncertainty를 의미하며 데이터가 많아도 감소시킬 수 없다(데이터 자체의 노이즈). 반면에 $\sigma_e^2$은 epistemic uncertainty를 의미하며 데이터의 수가 많아지면 감소시킬수 있는 uncertainty다.(lack of training data)

• low aleatoric, high epistemic: training data 부족

• high aleatoric, low epistemic: multiple possible steering angles

PROPOSED UNCERTAINTY ESTIMATION METHOD

$$p(y \ mid \theta) = \sum_{j=1}^K\pi_j(x)\mathcal{N}(y \mid u_j(x), \Sigma_j(x))$$

MDN의 output은 위와 같이 전개된다.

• $\pi_j, u_j, \Sigma_j$: j번째 가중치, 평균, 분산

[Note] density network에 비해서 MDN이 복잡하고 노이즈가 많은 distribution에 잘 학습된다.

MDN output의 분산을 구하기 위해서는 먼저 평균값에 대한 정보가 있어야 한다. 아래는 output의 평균에 대한 수식이다.

$$\begin{align} E[y \mid x]&=\sum_{j=1}^K\pi_j(x) \int \mathcal{N}(y\midu_j(x), \Sigma_j(x)) dy\\ &= \sum_{j=1}^K\pi_j(x)u_j({x}) \end{align}$$

분산식은 아래와 같다.

$$\begin{align} V[y\mid x] &= \int \rVert y-E[y\mid x]\rVert ^ 2p(y \mid x)dy \\ &= \sum_{j=1}^K\pi_j \int \rVert y-\sum_{k=1}^K\pi_k(x)u_k({x})\rVert ^ 2 \mathcal{N}(y \mid u_j(x), \Sigma_j(x)) dy \end{align}$$ $$\begin{align} \int \rVert y-\sum_{k=1}^K\pi_k(x)u_k({x})\rVert ^ 2 \mathcal{N}(y \mid u_j(x), \Sigma_j(x)) dy &=\int \rVert y-u_j\rVert ^ 2 \mathcal{N}(y \mid u_j, \Sigma_j) dy +\\ &\int \rVert u_j-\sum_{k=1}^K\pi_ku_k\rVert ^ 2 \mathcal{N}(y \mid u_j, \Sigma_j) dy \\ &+ 2\int(y-u)^T(u_j - \sum_{k=1}^K\pi_ku_k)\mathcal{N}(y \mid u_j, \Sigma_j) dy\\ &= \Sigma_j + \rVert u_j- \sum_{k=1}^K\pi_ku_k \rVert . \end{align}$$

위의 수식을 적용하면, 분산식은 아래와 같이 전개된다.

$$\begin{align} V[y \mid x] &=\sum_{j=1}^K\pi_j(x)\Sigma_j(x) + \sum_{j=1} ^ K\pi_j(x)\rVert u_j(x)- \sum_{k=1}^K\pi_k(x)u_k(x) \rVert^2 \end{align}$$

위에서 언급했듯이 total variance는 epistemic과 aleatoric으로 분리할수 있다. MDN은 조금 다르게 explainable variance와 unexplainable variance로 분리된다.

• $\sum_{j=1} ^ K\pi_j(x)\rVert u_j(x)- \sum_{k=1}^K\pi_k(x)u_k(x) \rVert^2 =E_{k \sim\pi}(V(y \mid x, k))$: epistemic uncertainty
• $\sum_{j=1}^K\pi_j(x)\Sigma_j(x) = V_{k \sim\pi}(E[y\mid x, k])$:aleatoric uncertainty