Batch Normalization에 대하여

Problem Define

학습하는 과정에서 이전 layer의 parameter가 변하면서, 각 layer의 input들의 distribution이 training과정마다 변하게 된다. 이런 문제는 학습이 불안정하게 하며, 낮은 learning rate를 사용해야 학습이 진행된다. 결론적으로는 saturating non-linearity의 모델을 학습하기 어려워진다. 이런 현상을 internal covariate shift 라고 부른다.

saturating non-linearity: 어떤 입력이 무한대로 갈 때 함수값이 어떤 범위내에서만 움직이는 것

ex) sigmoid

not-saturating non-linearity: 어떤 입력이 무한대로 갈 때 함수값도 무한대로 가는 것을 의미

ex) Relu

sigmoid activation에 대해서 생각해보면, 위의 문제가 왜 심각한지 알 수 있다. sigmoid function은 saturating function중 하나로 $\rvert x\rvert $가 증가할 수록 gradient값이 0에 수렴한다.

g(x)=11+exp⁡(−x)g(x) = \frac{1}{1 + \exp(-x)}

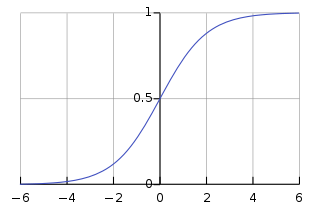
layer의 depth가 깊어질수록 이 문제는 더 커지게 되는데, 이런 문제를 해결하기 위해서 Relu를 많이 사용한다. 하지만, Batch normalizing을 사용하게 되면 stable한 distribution을 가지게 되어서 이런 문제를 해결할 수 있다.

Towards Reducing Internal Covariate Shift

deep learning model은 많은 layer가 연결되어 있는 구조이다. layer가 2인 모델을 가정해보면, 다음과 같이 수식으로 나타낼 수 있다. h1=F1(x)h_1 = F_1(x)

output=F2(h1)output = F_2(h_1)

where $h_1$ is hidden layer, $F_1$ is first layer, $F_2$ is second layer.

위의 구조에서 볼 수 있듯이 $F_2$는 $F_1$의 dependent 하다고 할 수 있다. 학습이 진행되는 과정을 보면 internal covariate shift에 대해서 알 수 있다.

  1. 첫번째 batch로 output을 구하고 실제 target과의 차이로 loss를 정의한다.
  2. loss를 바탕으로 gradient를 구한다.
  3. parameters를 update한다.

위의 1 ~ 3번의 과정을 반복하는게 학습의 과정이다. 하지만, 3번의 parameter update과정에서 $F_1, F_2$ layer가 변하게 되는데 이는 distribution이 변하는 것으로 해석할 수 있다. 직관적으로 생각해보면, $F_2$ layer는 update 되기전의 $F_1$을 바탕으로 학습을 진행했는데, 그 다음 step에서 갑자기 변한 $F_1$ layer를 바탕으로 학습을 진행해야 하는 것이다.

이렇게 학습이 진행되면, gradient step은 normalization이 진행되야되는 방향으로 학습이 진행되며 이는 gradient의 효과를 경감시킨다. 이는 아래의 수식 전개를 보면 확인할 수 있다. 해당 수식은 bias parameter만 가진다고 가정한다.

Notation

  • input: $u$
  • learned bias: $b$
  • activation computed over training set: $\hat{x} = x - E[x]$
  • $x=u +b$, $\mathcal{X} ={ x_{1 \cdots N} }$
  • $E[x] = \frac{1}{N}\sum_{i=1}^Nx_i$

만약 $E[x]$가 $b$에 미치는 영향을 무시하고 학습한다면, 아래와 같이 update된다.

b←b+∇bb \leftarrow b + \nabla b ∇b∝−∂l∂x^\nabla b \varpropto \frac{-\partial l}{\partial\hat{x}}

다음 feed forward 과정을 생각해보면 다음과 같다. ($b$는 update되기전 parameter) u+(b+∇b)−E[u+∇b]=u+b−E[u+b]u + (b + \nabla b) - E[u + \nabla b] = u + b - E[u + b] 위의 식에서 볼 수 있듯이 $\nabla b$가 사라짐으로써 학습효과가 없게 된다.

Fixed Distribution

이런 문제를 해결하기 위해서, 어떤 parameter 값들을 가지든 의도한 distribution이 나오도록 만들어야 한다. distribution이 고정되면, gradient가 normalization에 dependent하게 만들어진다.

notation

  • layer input: $x$
  • set of inputs over training set: $\mathcal{X}$
  • normalization: $\hat{x} = Norm(x, \mathcal{X})$

위의 normalization term은 training example $x$뿐만 아니라 모든 examples $\mathcal{X}$에 영향을 받는다. 만약 $x$가 이전 layer의 output이라면, $\mathcal{X}$은 이전 layer parameter에 영향을 받는다.

backpropagation 과정에서는 Jacobians를 계산해야한다.

(1) $x$에 대한 gradient ∂Norm(x,X)∂x\frac{\partial Norm(x, \mathcal{X})}{\partial x}

(2) $\mathcal{X}$ 에 대한 gradient ∂Norm(x,X)∂X\frac{\partial Norm(x, \mathcal{X})}{\partial \mathcal{X}}

만약 (2)를 고려하지 않게되면, 위에서 언급한 문제가 발생할 수 있다. 하지만 이는 매우 비싼 computation cost를 치뤄야 한다.

[covariance matrix] Cov[x]=Ex∈X[XXT]−E[x]E[x]TCov[x] = E_{x\in \mathcal{X}}[XX^T] -E[x]E[x]^T [inverse square root]: to produce the whitened activations Cov[x]−1/2(x−E[x])Cov[x]^{-1/2}(x - E[x]) 기타 backpropagation과정에서의 derivatives들도 많은 computation cost를 치뤄야한다.

어떻게 하면 합리적인 computation cost로 모델의 representation ability를 보존할 수 있을까?

Normalization via Mini-Batch Statistics

위에서 언급했듯이, 모든 layer의 input에 대한 full whitening은 computation cost가 높고, 미분가능하지 않을 수도 있다. 이런 문제를 해결하기 위해서 두가지 가정을 한다.

[whitening]

이는 기저벡터(eigenbasis) 데이터를 아이겐밸류(eigenvalue) 값으로 나누어 정규화는 기법이다. 화이트닝 변환의 기하학적 해석은 만약 입력 데이터가 multivariable gaussian 분포를라면 화이트닝된 데이터는 평균은 0이고 공분산(covariance)는 단위행렬을 갖는 정규분포를 갖게된다. 와이트닝은 다음과 같이 구할 수 있다:

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)
  1. layer의 input과 output의 feature를 jointly하게 구하는 것이 아니라, 각 feature를 독립적으로 mean=0, var=1을 가지도록 정규화한다. ($\hat{x}^{(k)}$는 각 layer의 input의 k번째 dimension 성분) x^(k)=x^(k)−E[x^(k)]Var[x^(k)]\hat{x}^{(k)} = \frac{\hat{x}^{(k)}- E[\hat{x}^{(k)}]}{\sqrt{Var[\hat{x}^{(k)}]}} decorrelated feature에도 불구하고 해당 normalization은 convergence 속도를 빠르게 한다고 알려져 있다.(Neural Networks: Tricks of the trade - 1998)

하지만, 기억해야 될 것은 normalizing이 layer의 representation능력에 변화를 준다는 것이다. 예를 들어, Sigmoid activation을 사용할 경우, -1 +1 사이로 normalizing이 진행되어 non-linearity의 특성을 잃어버리게 된다.

  1. 이 문제를 해결하기 위해서는 결국 normalizing이 같은 representation을 하도록 해야한다.

    $\hat{x}^{(k)}$는 activation을 의미하고 $ \gamma^{(k)}, \beta^{(k)}$는 parameter를 의미한다. 이 parameter는 학습시에 모델의 다른 parameter와 같이 학습되며 모델의 representation power를 유지하는 방향으로 학습이 진행된다. y^(k)=γ(k)x^(k)+β(k)\hat{y}^{(k)} = \gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)}

    만약 아래와 같이 파라미터 값을 지정한다면, 원래의 representation을 복원할 수 있다.

    γ(k)=Var[x(k)]\gamma^{(k)} = \sqrt{Var[x^{(k)}]}

    β(k)=E[x(k)]\beta^{(k)} = E[x^{(k)}] 일반적으로 Stochastic Gradient Training을 하기 때문에 각 mini-batch activation에 해당하는 variance mean를 사용하게 된다. 이는 normalization이 backpropagation과정에 적절히 관여하게 만든다.

중요한 점은 per-dimension variance를 구하는 것이 computation cost를 낮춘다는 것이다. (Singluar covariance matrices) 아래는 batch normalization algorithm에 대한 설명이다. 주목할 점은 learned parameter $\gamma, \beta$가 training example 뿐 아니라 mini-batch 안에 있는 다른 training example에 영향을 받는다는 것이다. ($\epsilon$은 stability를 위한 constant term이다.)

[Backpropagation 전개]

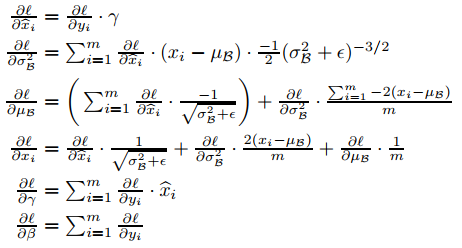
Training and Inference with BatchNormalized Networks

Training은 위와 같이 진행하면 되지만, inference를 할 때는 더 적절한 방법이 필요하다. 모델의 output이 input에 deterministic하게 나오도록 해야한다. 이를 위해서 다음과 같은 normalization이 필요하다. x^=x−E[x]Var[x]+ϵ\hat{x} =\frac{x-E[x]}{\sqrt{Var[x] + \epsilon}} 주목할 점은 여기서 나오는 $E[x], Var[x]$는 모두 mini-batch에서 얻은 것이 아니라 population에서 얻은 것이다. 위의 식에서도 mean=0, var=1로 유지된다. $Var[x]$는 sample variance $\sigma_b^2$로 부터 다음과 같이 구한다. Var[x]=mm−1⋅EB[σB2]Var[x] = \frac{m}{m-1}\cdot E_B[\sigma_B^2] training과정에서 moving average를 사용하는 것과 다르게 inference과정에서는 고정된 mean과 variance를 통해서 deterministic한 output을 도출한다. 이는 각 layer마다 linear transformation을 한 것으로 해석할 수 있다. 알고리즘은 아래와 같다.

Batch-Normalized Convolutional Networks

Affine transformation에 어떻게 적용될 수 있는지 살펴보자.

affine transformation

선형변환에 평행이동이 더해진 개념이다.

z=g(Wu+b)z = g(Wu + b)

where $g(\cdot)$ is non-linear such as sigmoid or Relu.

위의 수식은 inputs $u$에 대해서 $x=Wu + b$에 직접 Batch normalization을 적용할 수 있다. 이런 생각을 할 수 있다. input $u$에 batch normalization을 적용 할 수 있지 않을까? 하지만 문제가 있다. $u$는 결국 다른 non-linearity layer의 output이기 때문에 distribution이 training 과정마다 바뀐다. 그리고 첫번째 두번째에 제한을 한다고 해도 결국 covariate shift는 제거할 수 없다.

반면에, $Wu +b$는 symmetric, non-sparse distribution을 가진다. 따라서 이를 normalizing한다면 더 안정적인 결과를 얻을 수 있다.

위에서 언급했듯이 bias $b$는 backpropagation과정에서 무시될 수 있는데 이런 문제를 해결위해서 아래와 같이 위의 수식을 바꿀 수 있다. z=g(BN(Wu))z=g(BN(Wu)) 여기서 $BN$은 $Wu$의 각 dimention마다 독립적으로 적용되며, $\gamma^{(k)}, \beta^{(k)}$를 얻을 수 있다. ($k$는 각 dimension index를 의미한다.)

그렇다면, Convolution layer에서는 어떻게 적용될 지 살펴보자. 아래는 Convolution filter의 작동방법이다.

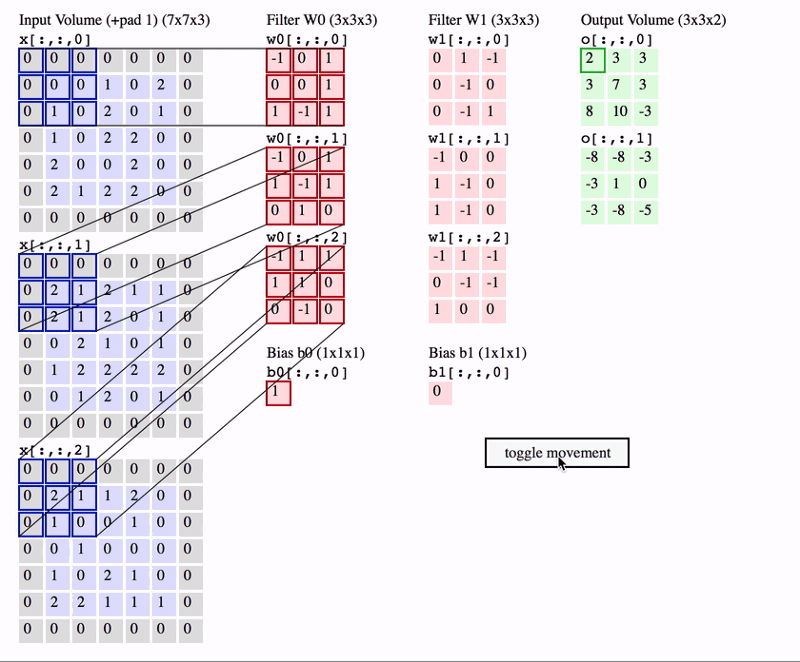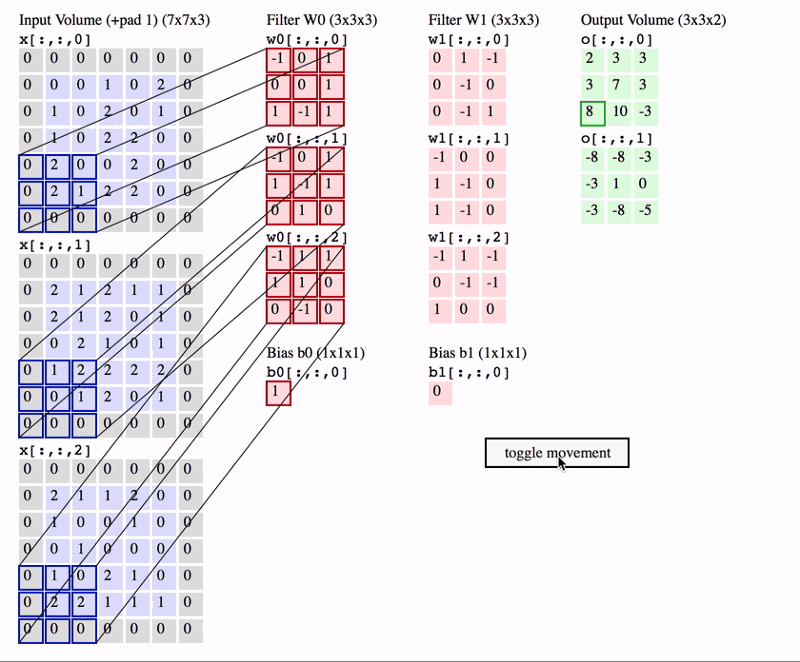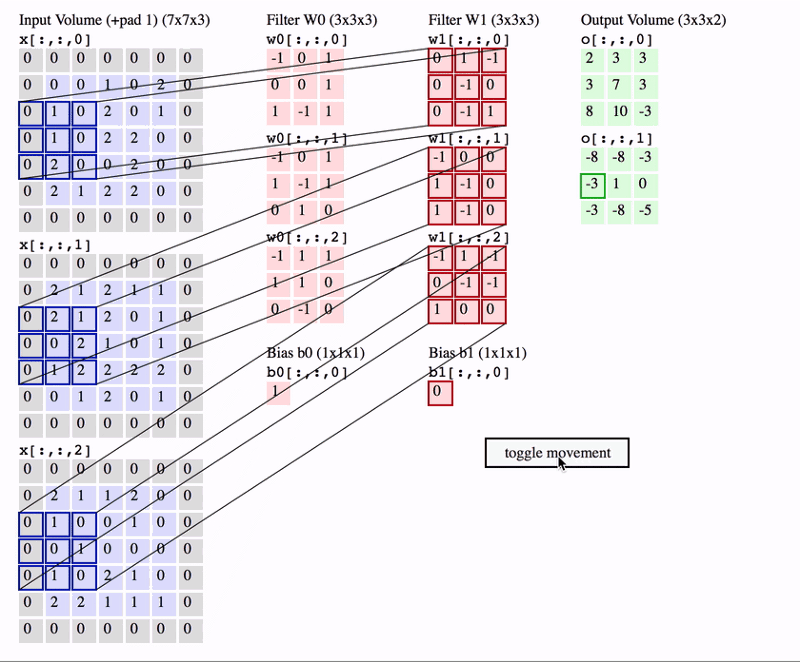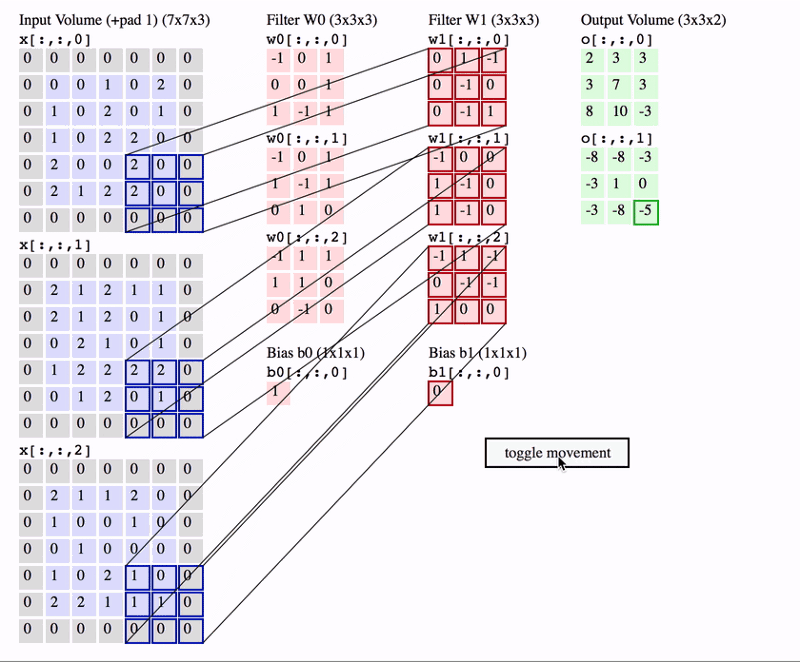
CNN의 특징중 하나는 ‘local connected’라는 것이다.

local connected

국지적인 정보의 집합을 이용하는 것을 의미한다. 즉 위의 그림처럼 filter안에 있는 정보끼리만 영향을 주며 filter가 이동할 때 이전 filter의 영향을 받지 않는다.

Convolution layer에서는 BN transformation이 다음과 같이 적용된다.

  • 추가적인 normalization이 필요하다. 이를 통해서 같은 feature map상에서 서로 다른 위치에 있는 구성요소를 공통적으로 normalize할 수 있다.

  • 이를 위해서 mini-batch상에 모든 activation을 location에 대해서 normalize를 진행한다. (jointly)

  • 아래의 Alg.1에서 $B$를 한 feature map에서의 각 location에 대한 activation value로 설정한다.(in mini-batch). mini-batch $B$의 크기는 feature map크기가 $p \times q$라고 가정하고 $m\cdot pq$가 된다. 따라서 $\gamma^{(k)}, \beta^{(k)}$는 activation마다가 아니라 feature map마다 구하게 된다.

Batch Normalization enables higher

Batch Normalization을 적용하면 더 높은 learning rate를 사용할 수 있으며, 이는 모델의 수렴속도를 높여준다.

일반적으로 parameter scale이 높으면, model explosion현상이 발생한다. 하지만, batch normalization을 사용하면 parameter scale의 영향을 받지 않는다. 또한 큰 parameter scale에도 smaller gradient를 가진다. BN(Wu)=BN((aW)U)BN(Wu) = BN((aW)U)

∂BN((aW)u)∂u=∂BN(Wu)∂u\frac{\partial BN((aW)u)}{\partial u} =\frac{\partial BN(Wu)}{\partial u} ∂BN((aW)u)∂aW=1a⋅∂BN(Wu)∂aW\frac{\partial BN((aW)u)}{\partial aW} =\frac{1}{a}\cdot\frac{\partial BN(Wu)}{\partial aW}

또한, 해당논문에서는 BN이 layer jacobians가 1에 가까운 singular value를 가진다는 것을 발견했다. (이는 train할 때 유용한 특성이다.)

  • normalized vector: $\hat{z} =F(\hat{x})$

  • 가정: $\hat{x}, \hat{z}$는 uncorrelated되어 있으며, gaussian을 따른다. 또한, 함수 $F(\hat{x}) \approx J \hat{x}$는 linear transformation이다.

  • $\hat{x}, \hat{z}$은 다음과 같은 covariance를 가진다. I=Cov[z^]=JCov[x^]JT=JJTI = Cov[\hat{z}] = JCov[\hat{x}]J^T=JJ^T 따라서, $JJ =I$이고 singular value는 1이다. 이는 gradient magnitude를 보존하는 역할을 한다.

    사실 real-world에서는 위의 가정이 사실이라고 하기 힘들지만 그래도 BN의 역할을 알 수 있다.

Batch Normalization regularizes the model

batch normalization은 Drop-out처럼 regularization효과가 있다.

Reference

  • https://arxiv.org/abs/1502.03167