Gradient Vector Valued Function

이번 글에서는 $f: R^n \rightarrow R^m$형태의 함수의 gradient에 대해서 다룰 것이다.

  • $f: R^n \rightarrow R^m
  • $x = [x_1, x_2, \cdots, x_n]$
  • $f_i: R^n \rightarrow R$
f(x)=[f1(x)f2(x)⋮fm(x)]∈Rmf(x) = \begin{bmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_m(x) \end{bmatrix} \in R^m

Partial Derivative of Vector Valued Function

위의 함수에서 $x_i$에 대해 편미분을 구해보면 아래와 같이 전개된다.

  • $x_i \in R$
∂f∂xi=[lim⁡h→0f1([x1,⋯ ,xi+h,⋯ ,xn])−f(x)hlim⁡h→0f2([x1,⋯ ,xi+h,⋯ ,xn])−f(x)h⋮lim⁡h→0fm([x1,⋯ ,xi+h,⋯ ,xn])−f(x)h]\frac{\partial f}{\partial x_i} = \begin{bmatrix} \lim_{h\rightarrow 0} \frac{f_1([x_1, \cdots, x_i + h, \cdots , x_n]) - f(x)}{h} \\ \lim_{h\rightarrow 0} \frac{f_2([x_1, \cdots, x_i + h, \cdots , x_n]) - f(x)}{h} \\ \vdots \\ \lim_{h\rightarrow 0} \frac{f_m([x_1, \cdots, x_i + h, \cdots , x_n]) - f(x)}{h} \end{bmatrix}

이제, vector $x$에 대해 미분을 구해보자. df(x)dx=[∂f∂x1,∂f∂x2,⋯ ,∂f∂xn]\frac{d f(x)}{d x} = \begin{bmatrix} \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \end{bmatrix}

위의 수식처럼, row vector형태로 나온다. 이를 더 전개해보면, 각 element는 column vector의 형태이므로 matrix 형태가 된다.

df(x)dx=[∂f∂x1,∂f∂x2,⋯ ,∂f∂xn]=[[lim⁡h→0f1([x1+h,⋯ ,xn])−f(x)hlim⁡h→0f2([x1+h,⋯ ,xn])−f(x)h⋮lim⁡h→0fm([x1+h,⋯ ,xn])−f(x)h],⋯ ,[lim⁡h→0f1([x1,⋯ ,xn+h])−f(x)hlim⁡h→0f2([x1,⋯ ,xn+h])−f(x)h⋮lim⁡h→0fm([x1,⋯ ,xn+h])−f(x)h]]∈Rm×n\frac{d f(x)}{d x} = \begin{bmatrix} \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} \lim_{h\rightarrow 0} \frac{f_1([x_1 + h, \cdots , x_n]) - f(x)}{h} \\ \lim_{h\rightarrow 0} \frac{f_2([x_1 + h, \cdots , x_n]) - f(x)}{h} \\ \vdots \\ \lim_{h\rightarrow 0} \frac{f_m([x_1 + h, \cdots , x_n]) - f(x)}{h} \end{bmatrix} , \cdots, \begin{bmatrix} \lim_{h\rightarrow 0} \frac{f_1([x_1, \cdots , x_n + h]) - f(x)}{h} \\ \lim_{h\rightarrow 0} \frac{f_2([x_1, \cdots , x_n + h]) - f(x)}{h} \\ \vdots \\ \lim_{h\rightarrow 0} \frac{f_m([x_1, \cdots , x_n + h]) - f(x)}{h} \end{bmatrix} \end{bmatrix} \in R^{m \times n}

Definition: Jacobian

함수 $f: R^n \rightarrow R^m$의 모든 first-order partial derivative의 모음을 jacobian이라고 한다. J=∇xf=df(x)dx=[∂f∂x1,∂f∂x2,⋯ ,∂f∂xn]∈Rm×nJ = \nabla_xf = \frac{d f(x)}{d x} = \begin{bmatrix} \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \end{bmatrix} \in R^{m \times n}

J(i,j)=fixjJ(i, j) = \frac{f_i}{x_j}

Jacobian: general way for identifying function.

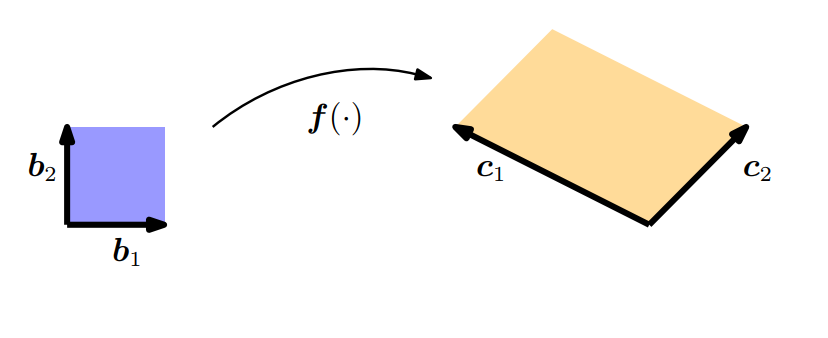
위와 같은 함수 f가 있다고 해보자. 각 $b_1, b_2$와 $c_1, c_2$는 아래와 같다.

  • $b_1 = [1, 0] ^T, b_2 = [0, 1]^T$
  • $c_1 = [-2, 1]^T, c_2 = [1, 1]^T$

domain 영역(파란색 부분) determinant는 아래와 같다. det⁡([1001])=1\det(\begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}) = 1

Codomain 영역(주황색 부분)의 determinant는 아래와 같다. det⁡([−2111])=−3\det(\begin{bmatrix} -2 & 1 \\ 1 & 1\end{bmatrix}) = -3

따라서, volume의 차이를 보면, 파란색보다 주황색 영역이 3배 크다. 위와 같은 mappingd을 모른다고 가정하고 두 가지 접근법을 통해서 구해볼 것이다.

  • linear algebra
  • vector calculus

1. Linear algebra: basis change

위의 mapping은 basis $b$에서 basis $c$로 바뀐 것으로 해석할 수 있다. 따라서 linear transformation matrix는 아래와 같다. J=[−2111]J = \begin{bmatrix} -2 & 1 \\ 1 & 1\end{bmatrix}

위의 matrix를 바탕으로 아래와 같은 관계를 구할 수 있다. Jb1=c1,Jb2=c2Jb_1 = c_1, J b_2 = c_2

그리고 $J$의 determinant는 $-3$으로 volume이 얼마나 늘었는지 알 수 있다.

2. vector calculus: partial derivative

linear algebra의 방법은 linear transformation에서만 가능하다는 한계를 가진다. 여기서 조금 더 general하게 접근할 수 있는 방법은 partial derivative를 활용하는 것이다.

함수 $f: R^2 \rightarrow R^2$의 partial derivative를 구할 것이다. coordinate를 살펴보면, 다음과 같은 관계를 구할 수 있다. (b1,b2)→(c1,c2)(b_1, b_2) \rightarrow (c_1, c_2)

y1=−2x1+x2y2=x1+x2y_1 = -2 x_1 + x_2 \\ y_2 = x_1 + x_2

이런 관계로 partial derivative를 구해보면 아래와 같다. ∂y1∂x1=−2,∂y1∂x2=1,∂y2∂x1=1,∂y2∂x2=1\frac{\partial y_1}{\partial x_1} = -2, \frac{\partial y_1}{\partial x_2} = 1, \frac{\partial y_2}{\partial x_1} = 1, \frac{\partial y_2}{\partial x_2} = 1 그리고 이를 바탕으로 jacobian을 구성해보면, J=[∂y1∂x1∂y1∂x2∂y2∂x1∂y2∂x2]=[−2111]J = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{bmatrix} = \begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix}

Geometric Interpretation of Jacobian

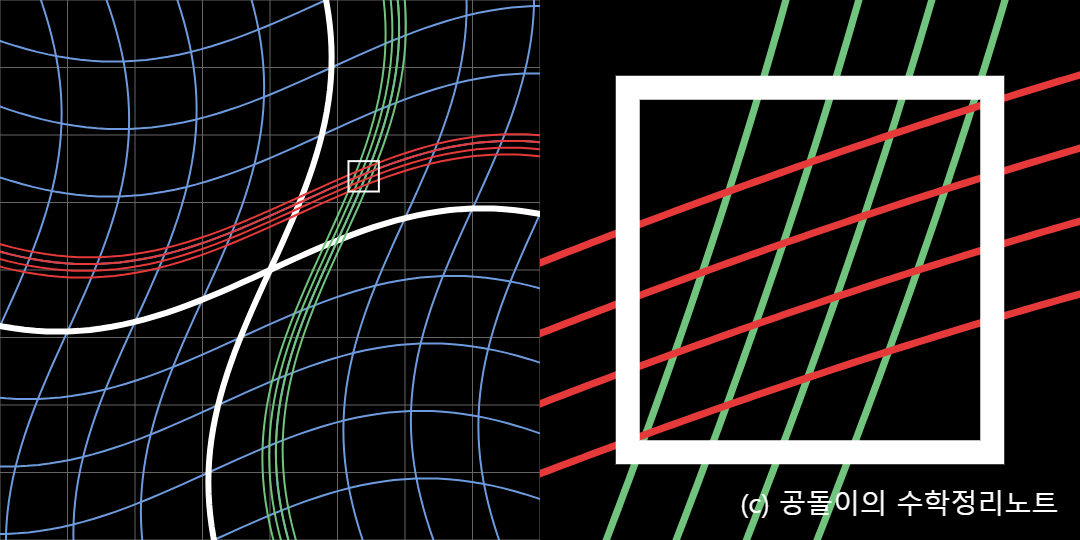
위의 이미지와 같이 non-linear transform이 있다고 했을 때, jacobian은 이를 linear하게 근사한 것이라고 볼 수 있다. 일반적으로 미분은 접선의 기울기라고 알려져 있는데, 이를 vector 공간에서 확장시키면 위의 이미지처럼, 나온다.

Reference

[1] 공돌이의 수학정리노트