LogSumExp Trick

머신러닝 학습을 진행하다보면, 종종 loss가 제대로 계산되지 않는 현상이 발생한다. 이는 loss를 계산하는 과정에서 불안정한 수식을 계산하기 때문에 발생한다. 특히 cross-entropy와 같이 log함수와 연관있는 수식은 주의가 필요하다.

아래 이미지는 로그 함수 그래프이다. 이 그래프에서 알 수 있듯이 $x$의 값이 0에 가까워질수록 $\log_2(x)$의 값은 음의 무한대의 값을 가지게 되며, 컴퓨터 연산과정에서 이는 연산이 불가능하다. (overflow)

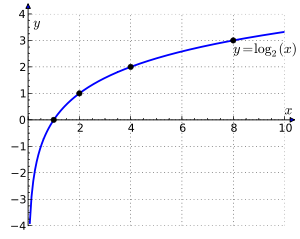
이러한 현상을 방지하기 위해서 사용하는 것이 LogSumExp trick이다.

LogSumExp (LSE) function is a smooth maximum – a smooth approximation to the maximum function, mainly used by machine learning algorithms.

$LSE(x_1, \cdots, x_n) = \log(\exp(x_1) + \cdots + \exp(x_n))$

LogSumExp는 convex function인데 따라서 loss 함수에 적용하기에 이론적으로도 적절하다.(http://www.math.uwaterloo.ca/~hwolkowi/henry/teaching/w10/367.w10/367miscfiles/pages48to60.pdf)

Numerical Stability

아래의 코드를 보면 $-1000$을 지수로 설정해도 안정성이 확보됨을 확인 할 수 있다.

>>> import math
>>> math.e ** -1000
0.0

Softmax

아래는 softmax의 수식이다.

exj∑i=1nexj\frac{e^{x_j}}{\sum_{i=1}^ne^{x_j}}

softmax는 특정 수를 non-linear한 방식으로 probability로 변환하는 것으로 해석할 수 있다. 이는 위의 LogSumExp pattern을 나타내고 있다.

\begin{align}\log\left(\frac{e^{x_j}}{\sum_{i=1}^{n} e^{x_i}}\right) &= \log(e^{x_j}) \:-\: \log\left(\sum_{i=1}^{n} e^{x_i}\right) \\ &= x_j \:-\: \log\left(\sum_{i=1}^{n} e^{x_i}\right) & (1)\end{align}

지수의 곱셈은 다음과 같이 전개된다. ea⋅eb=ea+be^a \cdot e^b = e^{a+b} 이는 log함수에서 다음과 같이 표현된다. log⁡(a⋅b)=log⁡(a)+log⁡(b)\log(a \cdot b) = \log(a) + \log(b) 위의 두 공식을 이용하면 LogSumExp의 공식은 아래와 같이 전개된다.

\begin{align} LogSumExp(x_1…x_n) &= \log\big( \sum_{i=1}^{n} e^{x_i} \big) \\ &= \log\big( \sum_{i=1}^{n} e^{x_i – c}e^{c} \big) \\ &= \log\big( e^{c} \sum_{i=1}^{n} e^{x_i – c} \big) \\ &= \log\big( \sum_{i=1}^{n} e^{x_i – c} \big) + \log(e^{c}) \\ &= \log\big( \sum_{i=1}^{n} e^{x_i – c} \big) + c & (2)\\ \end{align}

그렇다면, softmax에 적용해보자. 위에서 log softmax는 다음과 같이 전개되었다.

\begin{align} \log(Softmax(x_j, x_1…x_n)) &= x_j \:-\: LogSumExp(x_1…x_n) \\ &= x_j \:-\: \log\left(\sum_{i=1}^{n} e^{x_i}\right)\\ &= x_j \:-\: \log\big( \sum_{i=1}^{n} e^{x_i – c} \big) \:-\: c \end{align}

Logistic loss in Tensorflow

# sigmoid input: x
# output: y = 1 / (1 + exp(-x))
# 1 - y = exp(-x) / (1 + exp(-x))
# target: z 
import tensorflow as tf
Logistic_loss = -[z * tf.log(y) + (1 - z) * tf.log(1 - y)]

Logistic loss

= -[z * log(y) + (1-z) * log(1-y)]

= z * log(1 + exp(-x)) - (1-z) * [-x - log(1 + exp(-x))]

= z * log(1 + exp(-x)) + x + log(1 + exp(-x)) - z_x - z * log(1 + exp(-x))

= x - z_x + log(1 + exp(-x))

여기서 overflow를 피하기 위해서 tensorflow에서는 다음과 같이 수식을 변형한다.

LogisticLoss = max(x, 0) - z*x + log(1 + exp(-abs(x)))

여기서 절대값을 취해주는 이유는 overflow를 피하기 위해서이다. x가 만약 음수의 값을 가지면서 더 작아지면 exp(-x)의 값은 빠른 속도로 증가하게 된다.

def loss_func(y_true, y_pred):
    """Log sum exp tricks
    Check https://github.com/tensorflow/tensorflow/issues/172
    y_true: a * (abs(z1-z2)) + b, shape of [batch_size, ]
    y_pred: match, shape of [batch_size, ]
    """
    maxes = tf.where(tf.greater_equal(y_pred, 0),
                     y_pred,
                     tf.broadcast_to(0.0, shape=tf.shape(y_pred)))
    z_x = tf.multiply(y_true, y_pred)
    loglogit = tf.log(tf.broadcast_to(1.0, shape=tf.shape(y_pred))
                      + tf.exp(tf.clip_by_value(-tf.abs(y_pred), -1e-8, 0)))
    return maxes - z_x + loglogit
  • https://www.xarg.org/2016/06/the-log-sum-exp-trick-in-machine-learning/
  • https://github.com/tensorflow/tensorflow/issues/172
  • https://blog.feedly.com/tricks-of-the-trade-logsumexp/