Residual Variational Autoencoder: Anomaly Detection에 활용하기

• Residual Variational Autoencoder: Anomaly Detection에 활용하기
  • Introduction
  • Related Works
    • Residual Connection
    • Gradient Explosion in deep network
    • Anomaly detection based on Autoencoder
  • Anomaly detection based on Variational Autoencoder
  • Motivation
  • Method
    • Degradation: Residual Connection
    • Gradient Explosion: Gradient Clipping
  • Experiments
    • RAE vs AE
      • Train loss
      • AUROC
    • RVAE vs VAE
      • AUROC
  • Summary
  • References

Residual Variational Autoencoder: Anomaly Detection에 활용하기

Introduction

이번 포스팅은 마키나락스에서 내부적으로 개발한 Residual Variational Autoencoder에 대해서 작성하였습니다.

많은 딥러닝의 연구들은 비선형적인 레이어를 깊게 쌓으면서 좋은 성능을 보여줬습니다. 대표적인 예로, Resnet의 경우에 더 깊은 레이어를 효과적으로 쌓아 성능향상을 이루었습니다.

같은 맥락으로 Residual Variational Autoencoder은 레이어를 효과적으로 사용할 수 있도록 설계했습니다. 결과적으로 깊은 레이어를 통해 만들어진 정보압축을 통해서 anomaly detection에서 뛰어난 성능을 보여줬습니다.

아래의 글에서는 RVAE(Residual Variational Autoencoder)의 동기와 직면하였던 문제들에 대해서 설명드리고, anomaly detection 실험결과를 공유드리면서 글을 마치려고 합니다.

Related Works

Residual Connection

딥러닝 모델이 깊어지게 되면, 모델의 표현능력이 커지게 되며 train loss는 더 작아져야합니다. 하지만, 모델이 깊어지게 되면서 train loss가 더 증가하기도 하며, 이를 degradation이라고 정의합니다. 아래의 이미지는 degradation 문제를 보여줍니다. [4]

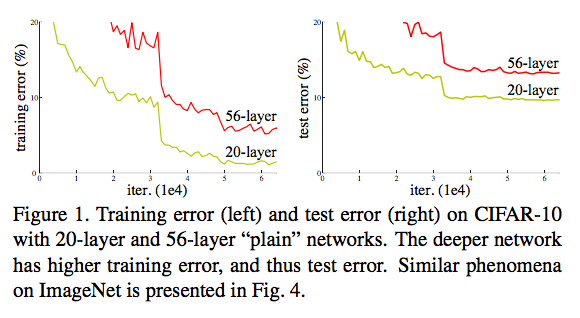
Resnet은 Residual connection을 통해서 Degradation 문제를 효과적으로 해결했습니다.[4]

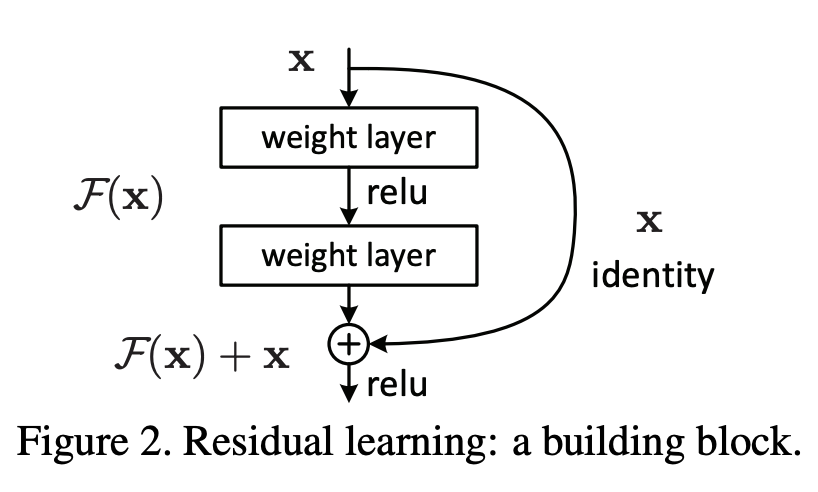
Residual Connection은 직관적으로는 레이어간의 지름길을 뚫어주는 효과를 줍니다. Residual Connection의 구조는 아래의 그림을 통해서 확인할 수 있습니다.

Gradient Explosion in deep network

gradient explosion이란 학습과정에서 backpropagation 도중에 gradient가 갑작스럽게 증가하는 현상을 의미합니다.

딥러닝 연구에서 일반적으로 비선형적인 레이어를 효과적으로 쌓으면, 모델 성능이 좋아지는 것을 보여줍니다. 하지만, 레이어를 깊게 쌓을 때, graidnet vanishing/explosion 문제가 발생하여 오히려 모델 성능이 하락하는 문제가 발생됩니다. [4, 5, 6, 7, 10]

Anomaly detection based on Autoencoder

anomaly detection에서 Autoencdoer구조는 많이 활용되고 있습니다.

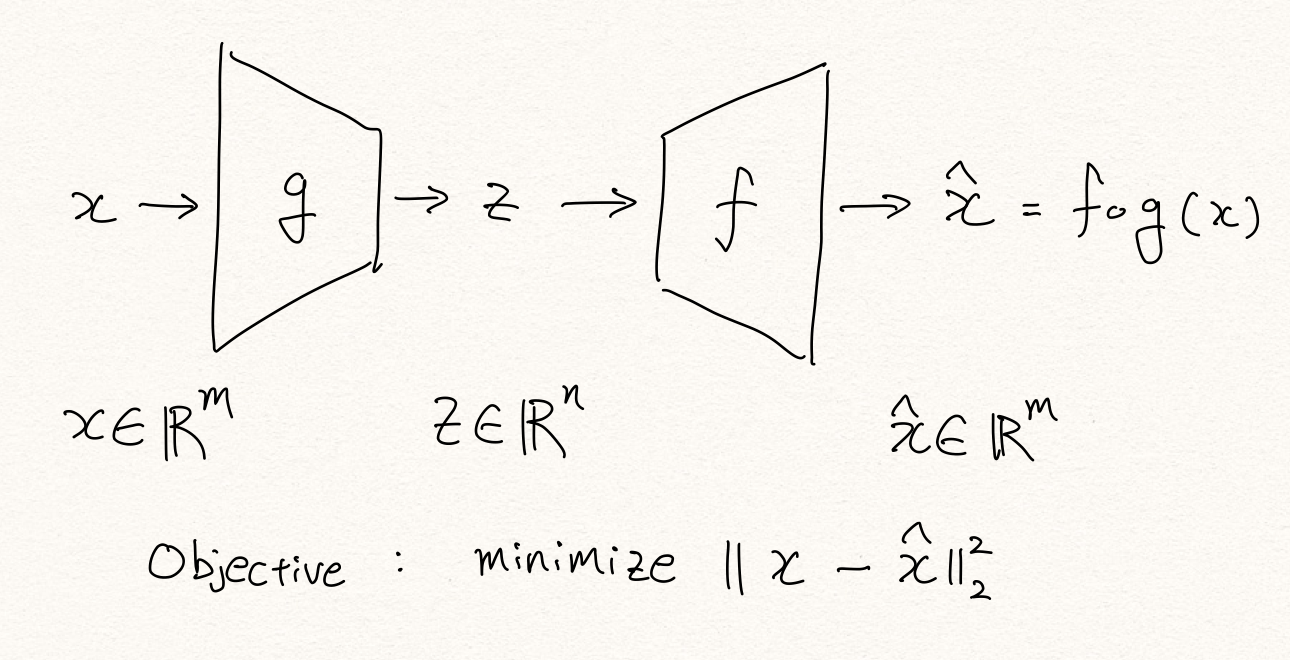
Autoencoder는 x 라는 고차원의 데이터를 저차원의 latent space(z)로 압축하고 이를 다시 $\hat{x}$ 로 복원시키는 구조이며, 이때 MSE(Mean Squared Error) $\rVert x - \hat{x} \rVert^2$을 최소화하는 방향으로 학습이 진행됩니다. manifold 가설에 따르면, Autoencoder는 input data의 noise를 제거하면서 의미있는 정보압축을 진행하는 방향으로 학습됩니다. [2]

이렇게 학습된 Autoencoder는 다음과 같은 과정을 통해서 anomayl detection을 수행합니다. [1]

• 입력 샘플을 인코더를 통해 저차원으로 압축합니다.
• 압축된 샘플을 디코더를 통과시켜 다시 원래의 차원으로 복원합니다.
• 입력 샘플과 복원 샘플의 복원 오차(reconstruction error)를 구합니다.
• 복원 오차는 이상 점수(anomaly score)가 되어 threshold와 비교를 통해 이상 여부를 결정합니다.

Anomaly detection based on Variational Autoencoder

variational autoencoder는 저자 Kingma가 2014년에 Auto-Encoding Variational Bayes [4]을 통해서 소개한 바 있습니다. variational autoencoder는 해당 논문에서 소개한 reparameterization trick을 통해서 인코더가 생성하는 $m, \sigma$ 로 latent variable $z$를 샘플링하고 이로부터 posterior distribuion $p(x | z)$ 를 근사하여 학습하게 됩니다. [1]

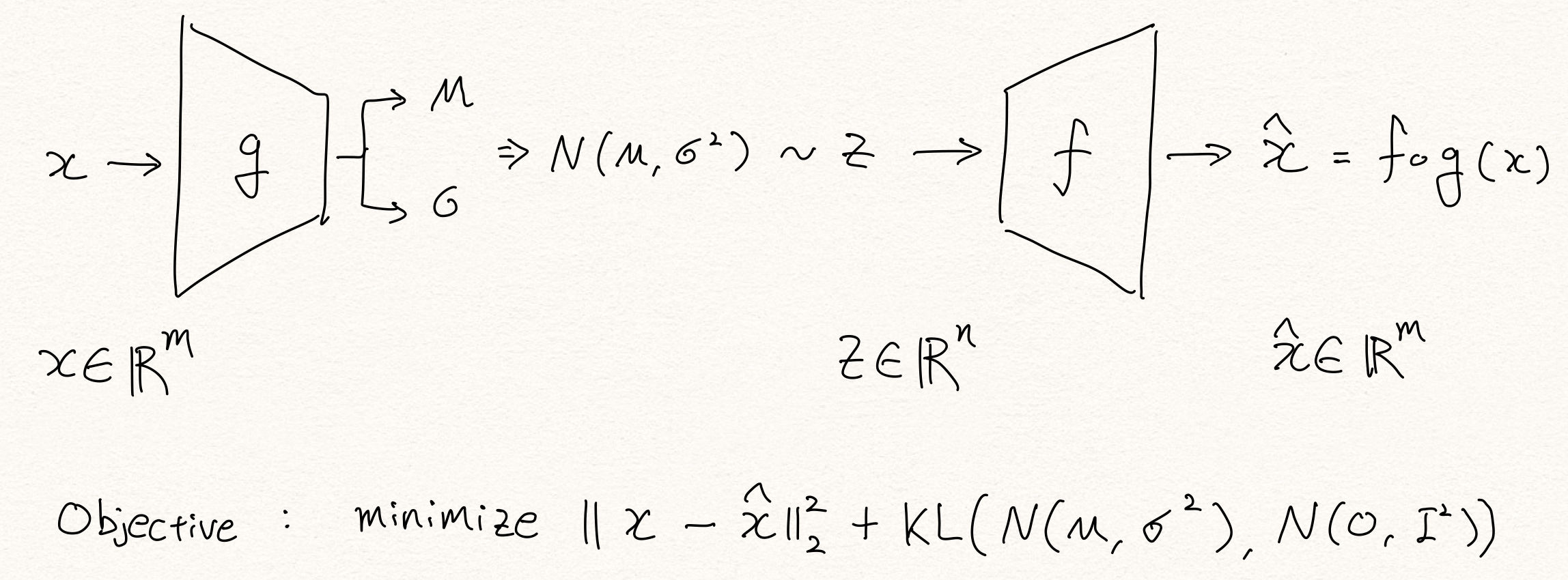
• $x \in R^n$: input data
• $z \in R^m$: latent variable
• $\hat{x} \in R^n$: reconstructed data

variational autoencoder에서는 MSE(Mean Squared Error)에 KLD 항을 더하여 loss function이 정의됩니다.

$loss_{vae} = \rVert x - \hat{x} \rVert ^ 2 + KL( \mathcal{N} (m, \sigma), \mathcal{N}(0, I))$

결론적으로 VAE는 MSE(reconstruction error)를 최소화하는 과정에서 KLD도 감소시켜야합니다. reconstruction error와 KLD는 서로 반대방향으로 움직이는 경향이 있습니다. KLD이 0이 된다면 input data에 대해서 독립적인 latent variable을 생성하게 됩니다. 그렇게 되면, reconstruction error가 높아집니다. 반대로, reconstruction error가 0이 된다면, KLD의 값이 커지게 됩니다. 정리하면, KLD의 역할은 VAE 모델이 x와 z가 적당히 연관되면서 reconstruction과 상관없는 정보를 더 잘 버릴수 있도록 하는데 있습니다. [1]

이처럼 KLD는 훌륭하게 regularizer의 역할을 하며 오버피팅을 막아줍니다. 결과적으로 이것은 마치 주어진 상황에서 최적의 병목 구간 크기를 갖게 하는 효과를 갖습니다. KLD를 통해 VAE는 vanilla autoencoder에 비해 훨씬 나은 성능의 이상탐지(anomaly detection) 성능을 제공합니다. 실험을 통해 우리는 기존의 autoencoder는 너무 큰 bottleneck을 가지면 identity function이 되며 이상탐지 성능이 떨어지는 것에 반해, VAE는 bottleneck의 크기가 커질수록 이상탐지 성능이 오르는 효과를 갖는 것을 확인할 수 있었습니다. 따라서 AE 기반의 anomaly detection을 수행할 때, 기존에는 bottleneck의 크기를 hyper-parameter로 튜닝해야 했던 반면에, VAE의 경우에는 튜닝을 할 필요가 거의 없어졌습니다. [1]

Motivation

AE(autoencoder)와 VAE(variational AE)는 휼륭한 결과를 보여줬습니다. 하지만, 레이어를 깊게 쌓을 수 없다는 한계가 있었습니다. 실험을 통해서, 레이어의 수가 특정 임계치를 넘어가면 레이어의 수가 늘어날 수록 train loss가 증가하는 현상이 발생하는 것을 확인했습니다. 우리는 이것을 degradation 문제로 정의했습니다. [4]

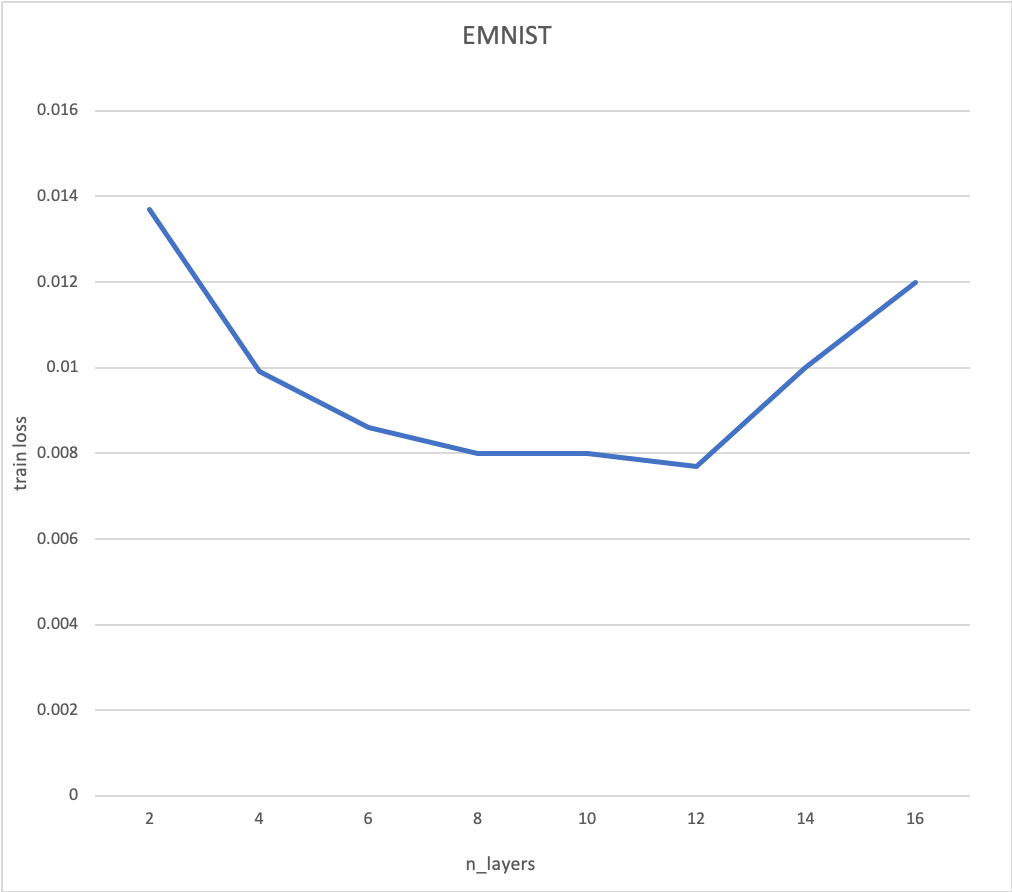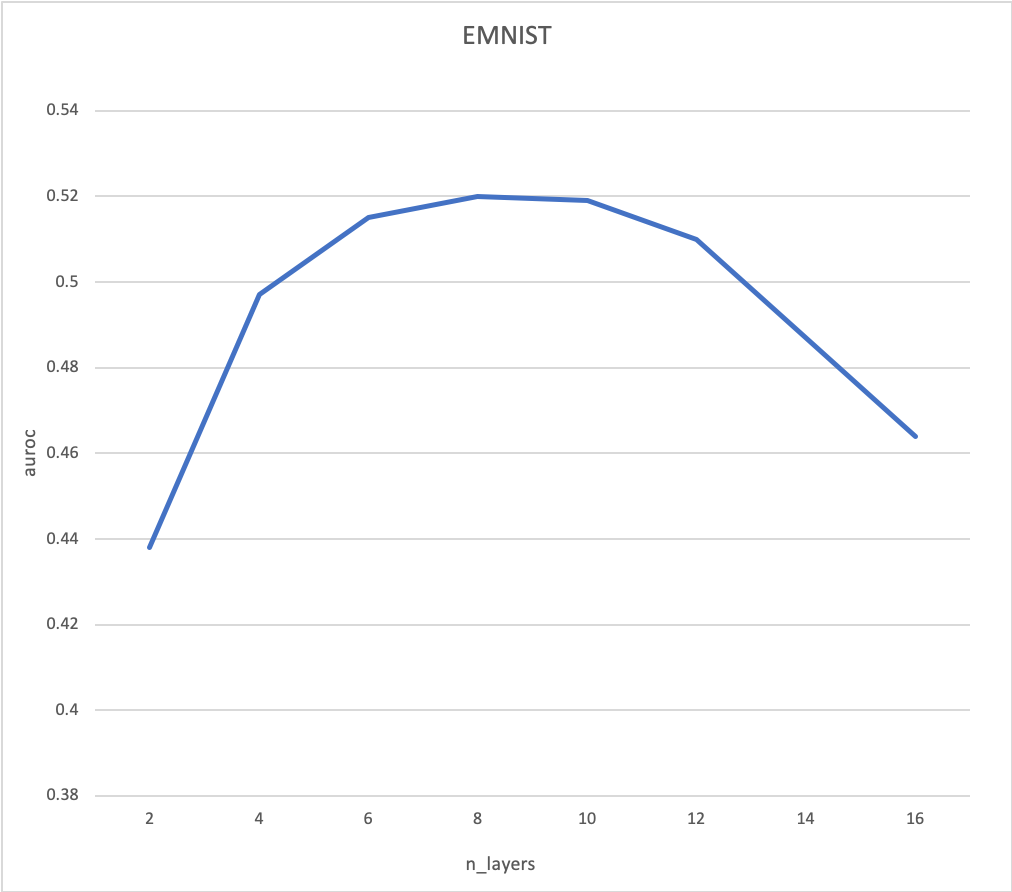위의 실험은 EMNIST 데이터셋을 바탕으로 anomaly detection의 실험환경에서 진행하였습니다. n_layers는 각 인코더, 디코더의 layer의 수를 의미합니다. 우리는 대칭적인 AE를 사용했으므로, 총 레이어의 수는 n_layers x 2 입니다.

효과적인 anomaly detection을 위해서는 일정수 이상의 레이어가 필요합니다. 이는 layer가 깊어질수록 더 많은 것을 고려한 압축과 복원작업을 학습하기 때문에, 더 의미있는 정보를 압축했다고 해석할 수 있습니다.

하지만, 기존의 AE에서는 레이어의 수가 임계치를 넘으면 train loss가 증가하며, auroc성능도 함께 하락합니다. 따라서 레이어를 쌓으면서 train loss를 줄이기 위한 방법이 필요합니다.

이를 위해서 Residual Connection을 고려했습니다. 더 깊은 레이어의 AE 혹은 VAE 구조를 효과적으로 학습하기 위해서 Residual connection을 고려하게 되었습니다. [4]

Method

본 섹션은 크게 3가지로 나누어서 설명드리겠습니다. 우리가 겪은 문제는 크게 3가지 입니다.

1. Degradation을 어떻게 해결할 것인가?
2. AE 구조에서 residual connection을 어떻게 구현할 것인가?
3. Residual AE에서 발생하는 gradient explosion은 어떻게 해결할 것인가?

Degradation: Residual Connection

Degradation 문제를 해결하기 위해서 Residual Connection을 활용하였습니다.[4] 일반적으로 residual connection을 사용하게 되면, gradient의 지름길이 뚫려서 멀리까지 전달되는 효과가 있습니다. residual connection은 결과적으로 gradient vanishing 문제를 효과적으로 해결 할 수 있으며 모델의 효과적인 학습에 기여합니다.

residual connection을 수식으로 나타내면 아래와 같습니다. [4]

$y_l = h(x_l) + \mathcal{F}(x_l, W_l) \\ x_{l+1} = f(y_l)$

• $x_l$: l-th residual unit
• $W_l = {w_{l, k} \mid 1 \le k \le K}$: l-th layer weight and bias
• $K$: the number of layers in reisudal unit
• $F$: reisdual function
• $f$: activation function

우리가 사용한 Residual connection 구조는 (b) proposed(identity)입니다.[8]

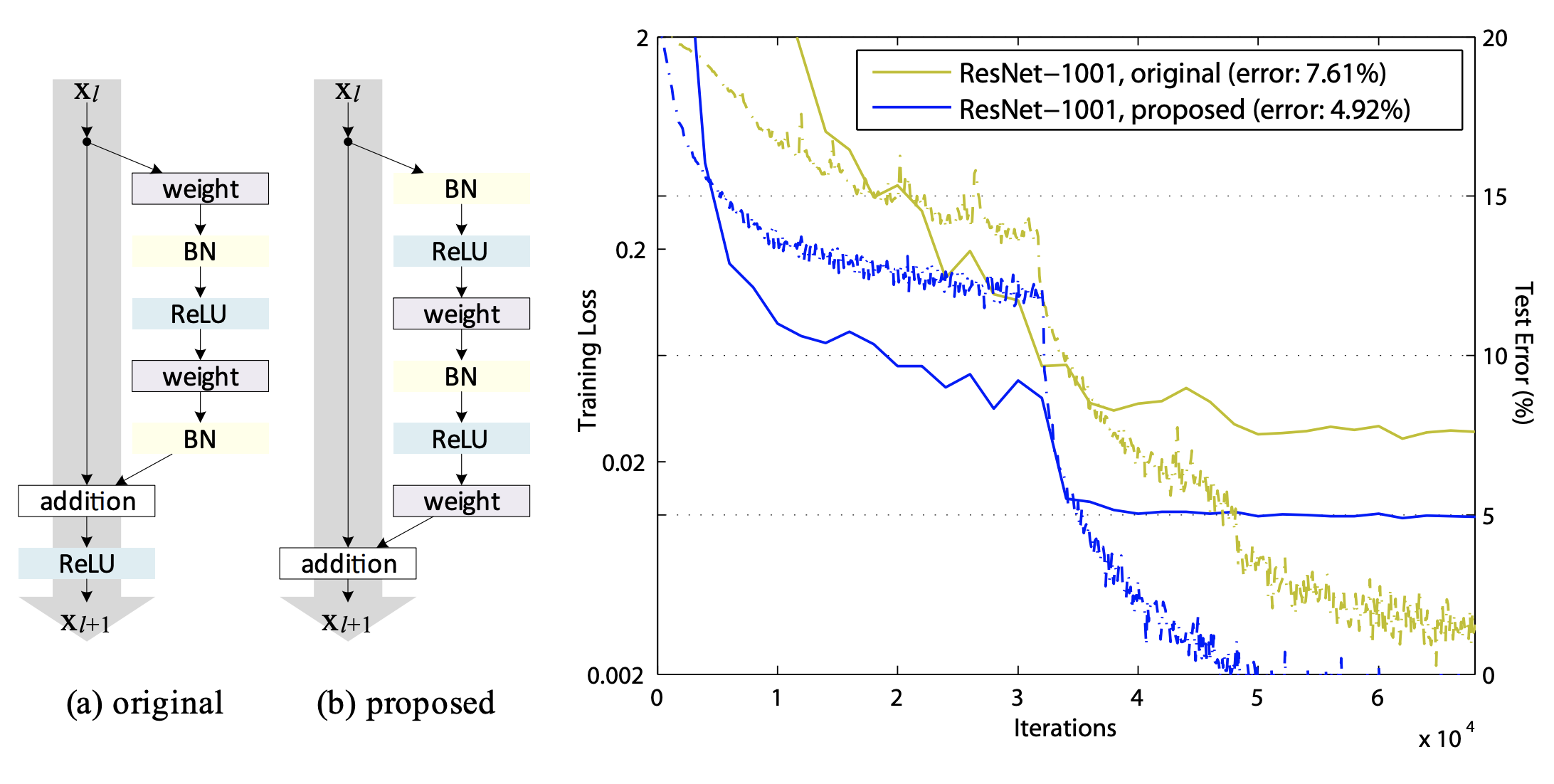
(b) proposed는 해당 identity 구조입니다.

identity mapping은 아래와 같은 관계를 가집니다.

$x_{l+1} = x_l + \mathcal{F}(x_l, W_l)$

이를 재귀적으로 풀어보면 아래와 같습니다.

$x_{L} = x_l + \sum_{i=l}^{L-1}\mathcal{F}(x_i, W_i)$

이처럼 identity mapping은 현재 레이어를 거쳐온 모든 레이어의 정보를 가지고 있다고 볼 수 있습니다. 그리고 이러한 관계는 backpropagation에서 근사한 특징을 가집니다. 미분하는 과정을 생각해보면, $x_L$이 $x_l$을 포함하기 때문에 $\frac{\partial x_L}{\partial x_l}$ 을 계산할 때, $\frac{Loss}{\partial x_L}$은 보존되게 됩니다.

$\frac{\partial Loss}{\partial x_l} = \frac{\partial Loss}{\partial x_L} \frac{\partial x_L}{\partial x_l} = \frac{\partial Loss}{\partial x_L}(1 + \frac{\partial}{\partial x_l}\sum_{i = l + 1}^{L-1}\mathcal{F}(x_i, W_i))$

이러한 특징은 degradation 문제를 매우 효과적으로 해결해줍니다. 따라서, 레이어가 깊어지더라도 train loss가 증가하는 폭을 낮출 수 있습니다.

우리는 이러한 identity mapping의 효과를 기대하며, 이를 AE에 적용했습니다.

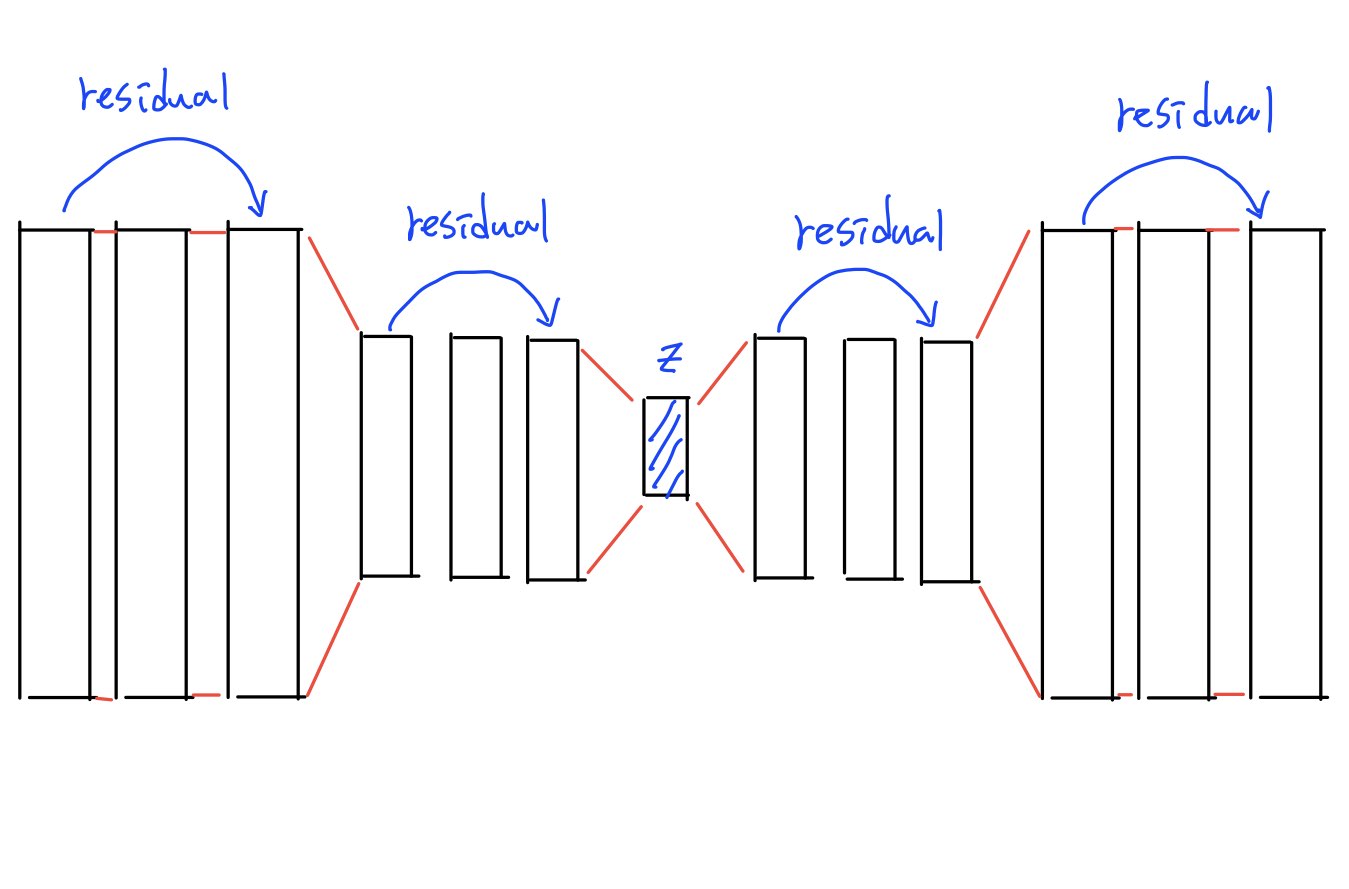
Gradient Explosion: Gradient Clipping

위의 과정을 거쳐서 residual AE/VAE가 완성되었지만, 해결해야 할 문제가 생겼습니다. 더 깊은 모델을 학습하는 과정에서 gradient explosion현상이 발생했습니다.[10] 이로 인해서 Residual Autoencoder를 학습할 때 아래와 같이 학습이 매우 불안정적으로 진행되었습니다. (g_norm은 gradient의 norm을 의미합니다.)

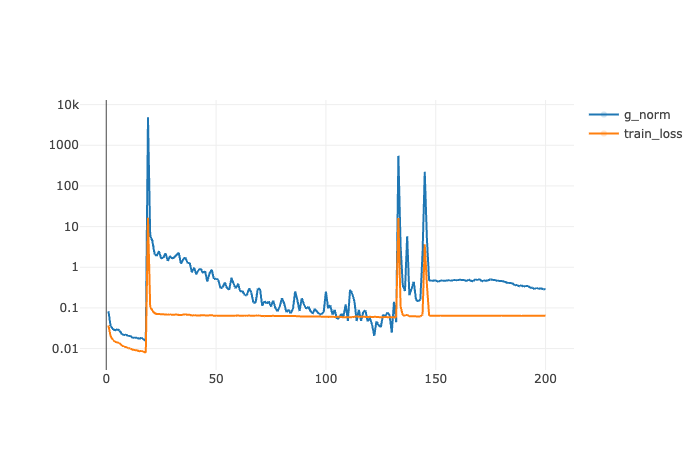
해당 그래프는 Residual AE를 MNIST데이터 셋을 학습시킨 결과입니다.

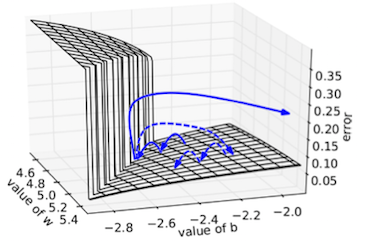
발생하는 원인에 대해서 loss surface가 아래와 같이 매우 극단적으로 나오는 것으로 추론할 수 있습니다.

이해를 돕기 위해서 아래와 같은 이미지로 설명드리겠습니다. 아래의 이미지는 모델의 파라미터가 $W \in R, b \in R$ 만 존재하는 경우의 loss surface입니다. 파란색 점은 모델의 파라미터에 대응하는 loss를 의미합니다. 학습이 진행되다가 loss surface가 매우 가파른 곳을 만나게되면, gradient의 값이 매우 커지게 됩니다. [7]

이를 해결하기 위해서 graidient를 clipping하여 사용했습니다. gradient clipping을 한다는 것은 weight가 학습되는 폭을 강제로 제한 하는 것입니다. 실제로 recurrent network를 학습시킬때 많이 활용하던 방법입니다. [12]

Experiments

실험은 Residual AE/VAE 모델의 성능을 검증하기 위해서 설계되었습니다. 모델 성능은 train loss와 anomaly detection의 auroc를 통해서 검증하였습니다.

실험파트는 크게 두 가지 내용을 검증합니다. 첫 번째로 AE 구조에서 Residual Connection이 degradation 문제를 해결하였는지 검증하였습니다. 이러한 결과를 바탕으로 anomaly detection에서 긍정적인 방향으로 적용되는지 실험하였습니다.

RAE vs AE

동일한 레이어의 대비 RAE와 AE 성능을 살펴보고, 각 모델의 최고 성능을 비교해보겠습니다. 실험에서 사용한 데이터셋은 EMNIST 이며, byclass의 데이터셋에서 0번 클레스를 anomaly class로 설정하였습니다. [14] 또한 anomaly class의 비율은 전체 데이터셋의 0.35로 고정시킨채 실험을 진행했습니다.

Train loss

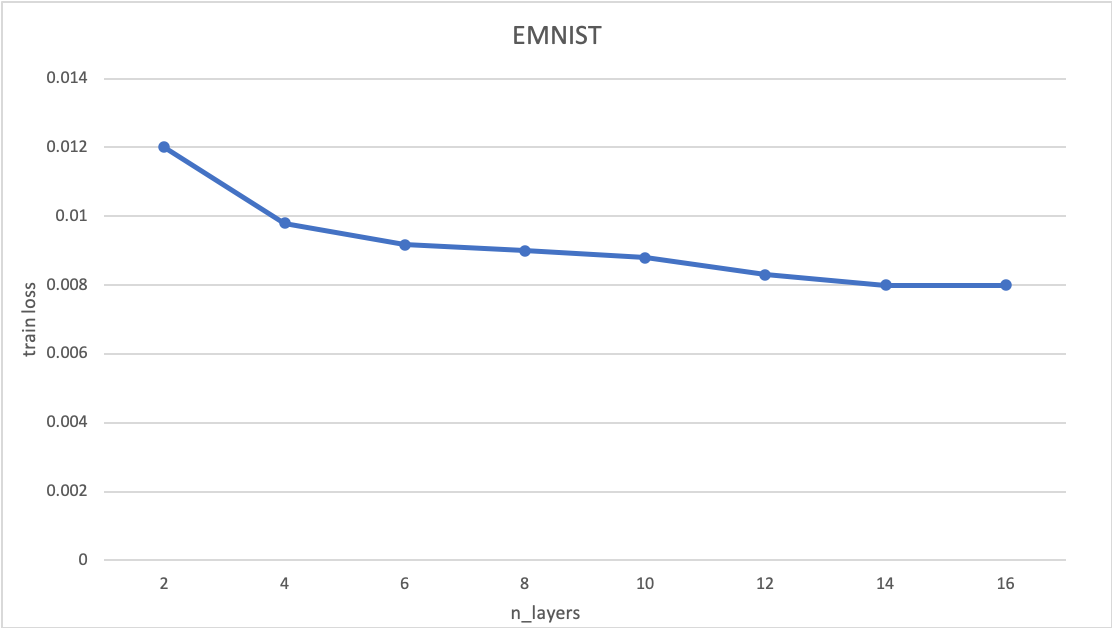
위의 그래프는 레이어의 수에 따른 train loss를 나타냅니다. 해당 결과는 AE 구조에서 나타나던 degradation 문제를 경감시킨 것을 보여줍니다.

AUROC

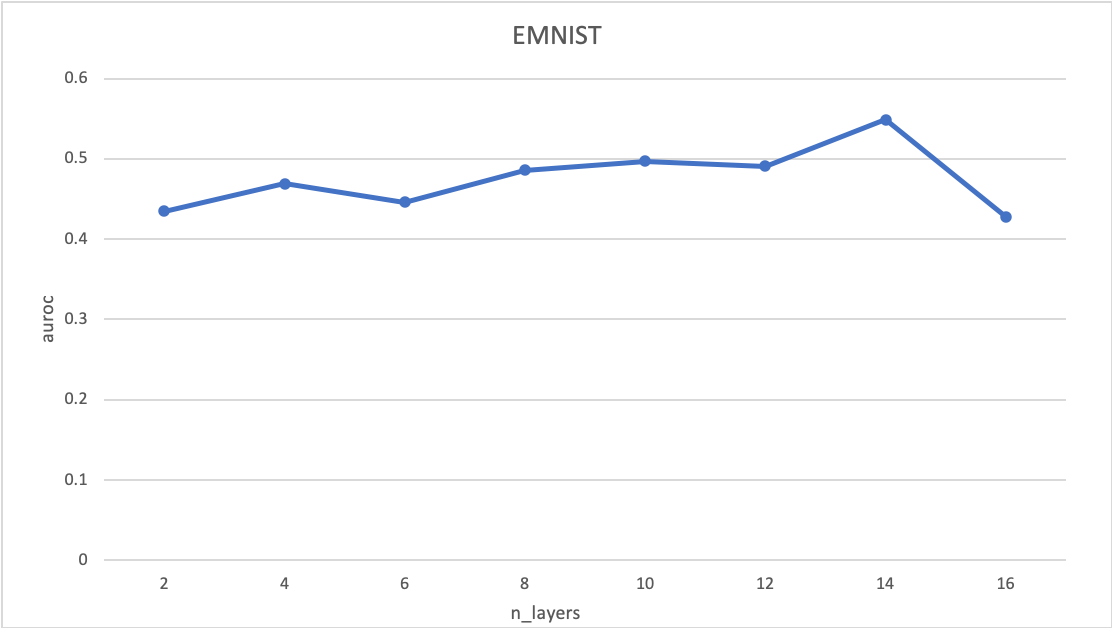
위의 그래프는 레이어 수 당 auroc를 나타냅니다. degradation 문제를 경감시키고 나서 anomaly detection에서의 성능을 확인해봤습니다. 아쉽게도 감소시킨 train loss가 auroc 성능향상에 도움을 줬으나, 일관성은 부족했습니다.

우리는 이것을 anomaly detection에서의 오버피팅이라고 생각하고 있습니다. n_layers = 6인 모델이 n_layers=4인 모델보다 복원에 필요한 압축은 잘하지만, 정상과 비정상을 나눌 수 있는 압축의 능력은 떨어졌습니다. 적절한 regularization이 더해진다면, 일관성 있는 결과가 나올 것으로 기대할 수 있습니다.

RVAE vs VAE

위에서 residual connection이 degradation 문제를 효과적으로 해결했음을 보였습니다. 이런 효과를 바탕으로 Residual VAE를 구현하여 실험했습니다. Variational AE, RVAE 같은 경우에는 KLD 값의 영향으로 train loss를 비교하는 것은 어렵습니다. 따라서 AUROC 성능으로 검증하도록 하겠습니다.

AUROC

아래의 실험은 SEED를 고정시키고 실험을 진행했습니다. 다른 논문의 VAE의 벤치마크 성능[13]과 비교해봤을 때, 큰 차이가 없는 것을 확인했습니다.

n_layers	RVAE	VAE
0	0.99	0.987
1	0.408	0.396
2	0.99	0.991
3	0.969	0.97
4	0.944	0.935
5	0.968	0.969
6	0.962	0.943
7	0.909	0.91
8	0.974	0.972
9	0.848	0.833

위의 실험결과를 통해서 RVAE 모델이 VAE모델보다 AUROC 성능을 향상 시킨 것을 확인했습니다. 실험결과를 보면 이렇게 해석할 수 있습니다. Residual Connection의 영향으로 레이어가 깊어져도 train loss는 낮게 유지할 수 있었습니다. 이는 상대적으로 큰 모델을 효과적으로 학습할 수 있음을 의미합니다. KLD를 활용한 regularization과 합쳐지면서 모델은 더 효과적인 압축을 진행할 수 있게 됩니다.

Summary

더 깊은 레이어를 쌓으면서 발생했던 degradation 문제와 이를 해결하기 위한 residual connection에 대해서 다뤄습니다. 또한, AE 구조에 residual connection을 적용하기 위한 노력들과 깊은 fully connected layer와 batch normalization을 같이 사용하면서 발생한 gradient explosion 현상을 해결하기 위해서 gradient clipping을 적용하였습니다.

결과적으로 RAE를 통해서 깊은 레이어의 모델에서 발생하는 degradation문제를 해결할 수 있었고, 여기에 KLD regularization을 적용하여 AUROC(anomaly detection 성능)을 높였습니다.

References

[1] Makinarocks: Autoencoder based Anomaly Detection

[2] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018

[3] Kingma et al., Auto-Encoding Variational Bayes, ICLR, 2014

[4] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016

[5] Y. Bengio, P. Simard, and P. Frasconi. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 5(2):157–166, 1994.

[6] S. Hochreiter. Untersuchungen zu dynamischen neuronalen netzen. Diploma thesis, TU Munich, 1991.

[7] X. Glorot and Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. In AISTATS, 2010

[8] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, 2016

[9] https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/

[10] Song Mei, Andrea Montanari, and Phan-Minh Nguyen. A mean field view of the landscape of two-layer neural networks. Proceedings of the National Academy of Sciences, 115(33): E7665–E7671, 2018.

[11] A. Veit, M. Wilber, and S. Belongie. Residual networks behave like ensembles of relatively shallow network. In NIPS, 2016.

[12] Pascanu, R., Mikolov, T., and Bengio, Y. (2013b). On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning (ICML 2013).

[13] Kim, K., Shim, S., Lim, Y., Jeon, J., Choi, J., Kim, B., Yoon, A., 2020. Rapp: Novelty Detection With Reconstruction Along Projection Pathway. ICLR 2020

[14] Cohen, G., Afshar, S., Tapson, J., & van Schaik, A. (2017). EMNIST: an extension of MNIST to handwritten letters. Retrieved from http://arxiv.org/abs/1702.05373