Mixup 정리글

• Mixup: Beyond Empirical Risk Minimization
  • Empirical Risk Minimization(ERM) VS Vicinal Risk Minimization(VRM)
  • Contribution
  • From Empirical Risk Minimization To Mixup
    • [what is mixup doing?]
  • Experiments
    • 3.1 IMAGENET CLASSIFICATION]
    • 3.2 CIFAR10 AND CIFAR100
    • 3.3 SPEECH DATA]
    • 3.4 MEMORIZATION OF CORRUPTED LABELS]
    • 3.5 ROBUSTNESS TO ADVERSARIAL EXAMPLES
    • 3.6 TABULAR DATA
    • 3.7 STABILIZATION OF GENERATIVE ADVERSARIAL NETWORKS
    • 3.8 ABLATION STUDIES

Mixup: Beyond Empirical Risk Minimization

mixup은 deep learning model의 memorization문제나 adversarial examples에 민감한 이슈를 해결하기 위해 나온 Data Augmentation기법입니다.

• memorization:

모델이 학습을 진행할 때, 정답만을 기억하고 내리는 행동. 즉, 데이터 분포를 학습하는 것이 아니라 해당 데이터가 어떤 라벨에 해당하는지 기억하게 되는 것. 결론적으로는 test distribution에 대한 generalization을 하지 못한다.

• sensitivity to adversarial examples: adversarial attack에 취약하다.

mixup은 network를 data pair간의 convex combination을 이용하여 학습시킵니다. 이는 결과적으로 모델이 training sample간에 simple linear behavior를 하지 않도록 하는 효과가 있습니다.

• simple linear behavior between training examples:

Empirical Risk Minimization(ERM) VS Vicinal Risk Minimization(VRM)

[성공적인 neural networks의 두 가지 특징]

1. trained as to minimize their average error over the training data.

2. the size of neural networks scales linearly with the number of training examples.

하지만, learning thoery에 따르면 ERM의 수렴은 모델의 복잡도가 데이터의 수보다 크지 않을 때 보장된다. 이는 [2]번 조건과 모순되어 보일 수 있으나 overfitting issue를 고려해보면 이해가 된다.

[memorization의 측정] adversarial examples에 예측하는 라벨이 크게 변하는 정도가 클수록 memorization이 크다고 평가할 수 있다. 직관적으로 생각해보면, 사람의 지각으로는 큰 차이가 없는 데이터에 대해서 딥러닝 모델이 서로 다른 예측을 한다면 이는 generalization을 못한 것으로 평가할 수 있다.

[Vicinial Risk Minimization이란] data augmentation의 이론적 배경으로 training data와 유사한 주변 데이터를 묘사하는 것이다. 이것이 가능해지면, virtual example(만들어진 데이터)는 training distribution의 support를 확대하는 효과를 가져온다. (training distribution중 모호한 부분을 채워주는 것으로 해석)

참고: [support of distribution]

Contribution

$X_{new} = {\lambda}X_i + (1 - {\lambda})X_j$ $Y_{new} = {\lambda}Y_i + (1 - {\lambda})Y_j$

위의 수식대로 data augmentation을 하는 것이 mixup의 전부이다.

아래의 영상은 lambda값에 따라서 mixup 데이터의 pca결과값이 어떻게 변하는지 시각화한 것이다. 아래의 그림들처럼 linear하게 PCA value가 변하는 것을 확인하였는데 이는 VRM 가정이 옳다는 것을 보여준다.

From Empirical Risk Minimization To Mixup

Supervised learning에서의 task는 결국 random feature vector X와 random target vector Y간의 관계를 설명할 수 있는 함수 f를 찾는 것이다. 함수 f는 joint distribution P(X, Y)를 따른다. 이 때, loss function의 역할은 prediction f(X)와 target Y간의 차이를 나타내며 학습을 진행하면서 average loss를 감소시킨다. 여기서 average loss는 expected risk으로 해석된다. 이를 수식으로 나타내면 아래와 같다.

${R}(f) = \int {loss}({f}(x), y)dP(x,y)\ \ [1]$

하지만, distribution P는 실제상황에서 알기 힘들다. (intractable distribution) 이를 해결하기 위해서 empricial distribution으로 근사하는 방법론을 이용한다. 이를 수식으로 나타내면 아래와 같다.

${P}_{\sigma}=\frac{1}{n}\Sigma_{i=1}^{n}\sigma(x={x}_i, y={y}_i) \ \ [2]$ $\sigma(x={x}_i, y={y}_i) 는\ Dirac\ mass\ centered \ at\ (x_i, y_i)\ 성질을 가지고 있다.$

[1]수식에 [2]수식을 대입하면 아래와 같이 전개될 수 있다.

참고: Dirac mass centered 아래 그림과 같이 굉장히 naive한 가정이다.

$R_{\sigma}=\int loss(f(x), y)dP_{\sigma}(x,y)=\frac{1}{n}\Sigma_{i=1}^{n}loss(f(x_i),y_i)$

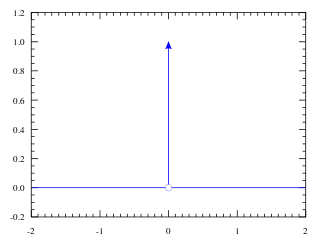
위와 같이 ERM은 간단하게 계산될 수 있지만, Memorization이라는 현상을 야기할 수 있다. joint distribution P에 어떤 가정을 하느냐에 따라서 결과가 달라질 수 있는데 이 논문에서는 Vicinal Risk Minimization Principle을 적용하고 있다. VRM을 가정하게 되면 P는 다음과 같이 정의할 수 있다.

$P_v(\tilde{x}, \tilde{y})=\frac{1}{n}\Sigma_{i=1}^{n}V(\tilde{x}, \tilde{y} \mid x_i, y_i) \ \ \text{where V is a vicinity distribution}$

vicinity distribution은 만들어낸 feature-target pair의 probability를 측정한다. 즉, 얼마나 그럴듯한 데이터인지 판단하는 것이다.

[what is mixup doing?]

(Mixup) Effect of mixup on a toy problem. Green: Class 0 Orrange: Class 1 Blue shading indicates $P(y = 1 \mid x)$.

위의 그림을 통해서 할 수 있듯이, mixup은 uncertainty를 측정하는데 더 효과적이다. 파란색 부분은 해당 데이터 x가 주어졌을 때, Class 1일 확률이다. ERM을 보면 파란색 부분이 Class 1가 가까운 것과 가깝지 않는 것 사이의 차이를 나타내지 못한다. 반면에 mixup은 가까운 부분은 더 짙은 파란색으로 나타내어, uncertainty를 smoother하게 측정할 수 있다.

(a) 는 prediction을 나타낸 것이고, (b)는 gradient norm을 나타낸 것이다. (a)를 보면 mixup으로 학습시킨 것이 더 prediction측면에서 좋은 성능을 보이고 있다.

한편, (b)를 보면 gradient norm이 더 작게 나는 것을 알 수 있는데, 이는 더 안정적인 학습을 보이고 있다는 것을 보여준다.

참고: norm

• 일반적으로 크기 혹은 길이를 나타낸다.

Experiments

3.1 IMAGENET CLASSIFICATION]

evaluation과정에서 224 * 224 크기의 중간부분이 소실된 이미지를 test하였다. 실험결과 hyperparameter alpha는 0.1에서 0.4사이의 값이 우수한 성능을 보였으며, alpha값이 이보다 더 크면 underfitting의 부작용을 가져왔다. 또한 mixup은 higer capacities와 longer training run의 효과를 가져왔다. 이는 ERM과 비교했을 때 , epoch 90에서 mixup이 더 큰 성능개선효과를 보였다는 것으로 증명하였다.

3.2 CIFAR10 AND CIFAR100

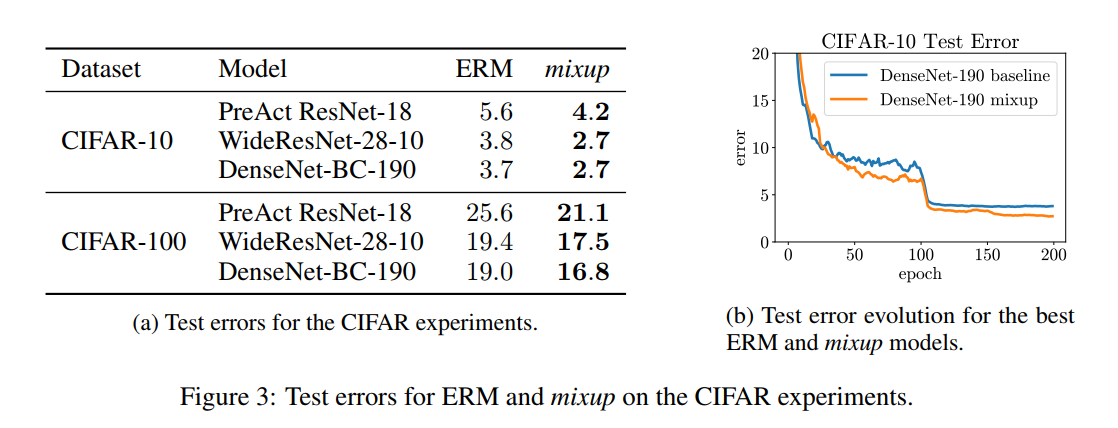
3.3 SPEECH DATA]

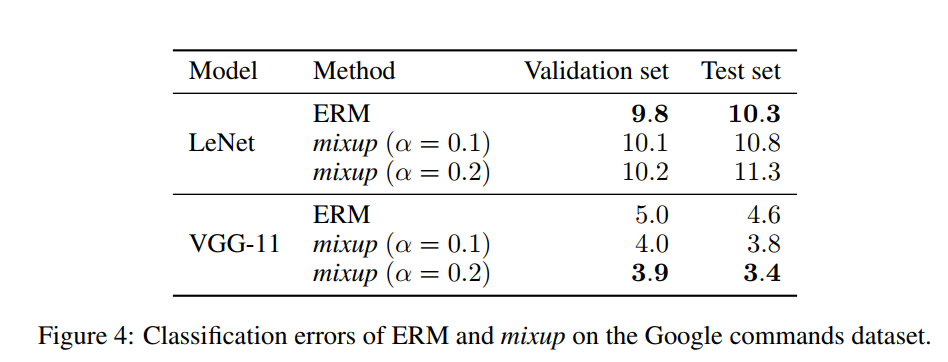
3.4 MEMORIZATION OF CORRUPTED LABELS]

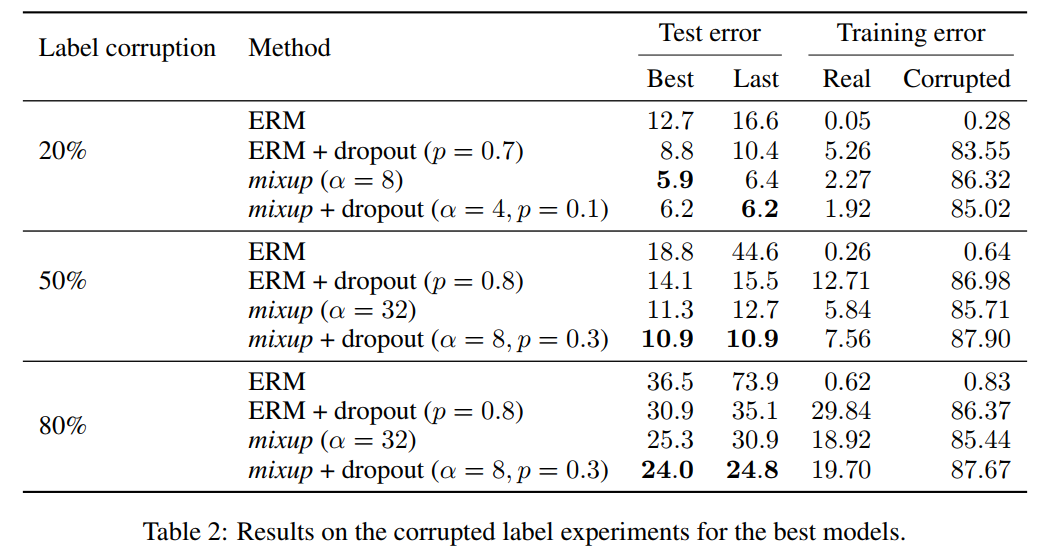
mixup interpolation alpha가 더 커질수록 memorization이 더 어려워진다는 가설을 세웠다. corruption label을 가지고 학습을 시켰다. 이는 memorizaiton을 검증하는 실험에서 사용된다. (더 찾아보기) 실험결과 test과정에서 large alpha가 dropout(0.7, 0.8)보다 test error를 더 줄일 수 있었으며, real label에 대해서는 낮은 training error를 보이고 noisy label에 대해서는 높은 training error를 보였다. 주목할 점은 dropout과 mixup을 같이 사용했을 때 성능이 가장 좋았다.

3.5 ROBUSTNESS TO ADVERSARIAL EXAMPLES

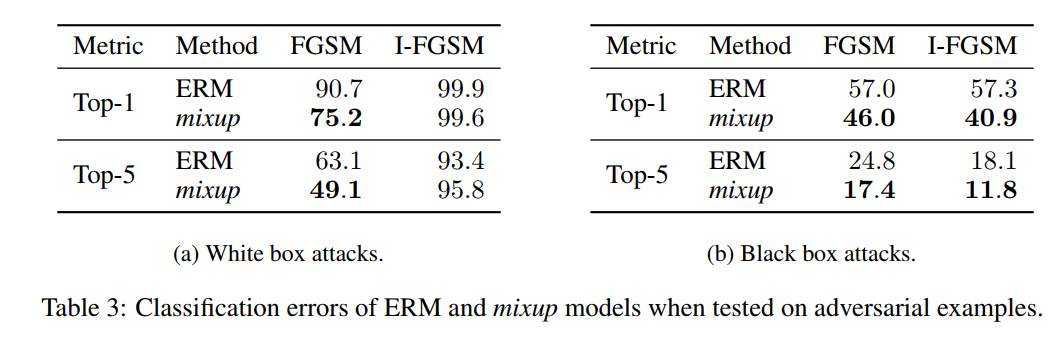
3.6 TABULAR DATA

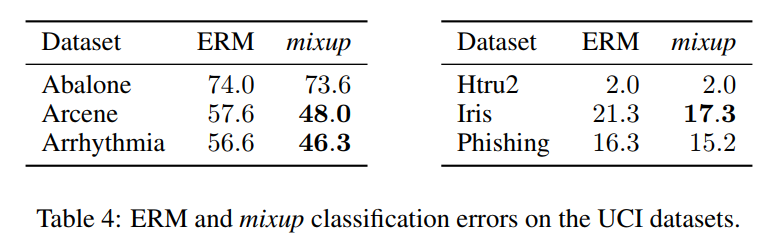
3.7 STABILIZATION OF GENERATIVE ADVERSARIAL NETWORKS

mixup은 disciriminator의 gradient regularizer의 역할을 하기 때문에, 더 안정적인 학습을 할 수 있다.

$\max_g\min_d E_{x, z}\mathcal{l}(d(x), 1) + l(d(g(z)), 0)$

기존의 GAN objective

아래는 mixup이 적용된 GAN distriminator objective이다.

$max_gmin_dE_{x, y, \lambda}l(d(\lambda x + (1-\lambda)g(z), \lambda).$

3.8 ABLATION STUDIES

이 논문에서는 convex combination을 통한 data augmentation방법론을 제안했지만, 다양한 방법론이 있을 수 있다.

[예시]

• feature map을 섞는다.
• 같은 클레스의 데이터
• 비슷한 거리에 있는 데이터
• 다른 클레스의 데이터

실험결과 현 논문에서 제시한 mixup이 제일 좋은 성능을 보였다.