직관적인 개념을 정리할 때, 일반적인 방법은 object 집합을 정의하고 그 object를 조작하는 방법에 대해서 서술하는 것이다. 이런 방법이 바로 ‘algebra’ (대수학)이다. 그 중 linear algebra는 vector에 대한 것이며, vector를 조작하는 것에 대해서 서술한다.

일반적으로 많이 들어본 것은 기하백터(Geometric Vector)일 것이다. 하지만, 이 책에서는 조금 더 일반적인 의미의 vector를 다룬다.

아래의 것들은 모두 vector이다.

  • Closure 성질: vector는 vector끼리 더해도 vector이며, scalar 값을 곱해도 vector여야한다.

  1. Geometric Vector

    두 개의 geometric vectors $\vec{x}, \vec{y}$ 를 더해도 여전히 geometric vector이며, scalar값을 곱해도 geometric vector이다.

  2. Polynomials

    다항식끼리 더해도 다항식이며, scalar 값을 곱해도 여전히 다항식이다.

  3. Audio signals

    audio signals는 숫자를 나열하여 표현할 수 있다. 두 개의 audio signal을 합쳐서 다른 audio signal을 만들 수 있으며, 한 audio signal의 scale을 증가시켜도 여전히 audio signal이다.

  4. Elements of R^n a=[123]∈R3a = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \in R^3 $a, b \in R^n$을 서로 더해도 vector이며, scalar 값을 곱해도 여전히 vector이다.

linear algebra mind map

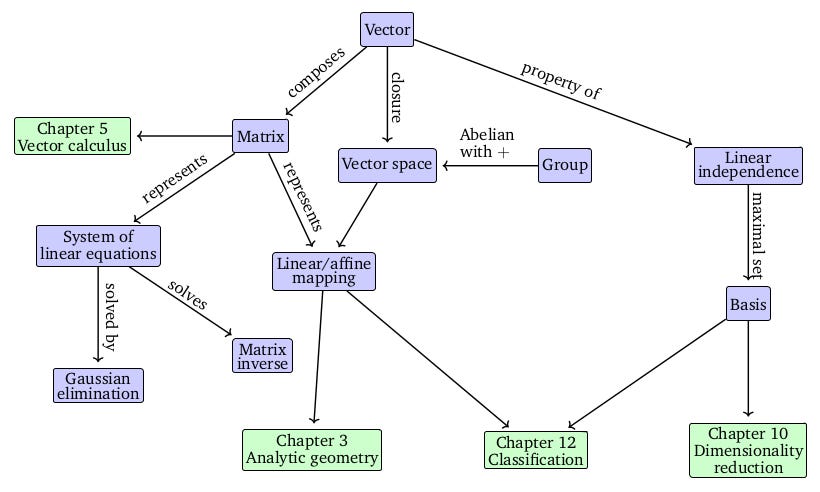
2.1 Systems of Linear Equations

아래와 같은 문제가 있다고 가정해보자. \begin{equation} a_{11}x_1 + \cdots + a_{1n}x_n = b_1 \\ \cdot \\ \cdot \\ \cdot \\ a_{m1}x_1 + \cdots + a_{mn}x_n = b_m \end{equation}

  • $a_{ij} \in R$, $b_i \in R$

위와 같은 문제는 linear equation으로 쉽게 해결할 수 있다. 위의 식은 아래처럼 나타낼 수 있다. 이는 vector와 scalar의 곱으로 나타낸 것이다. x1[a11⋅⋅⋅am1]+x2[a12⋅⋅⋅am2]+⋯+xn[a1n⋅⋅⋅amn]=[[b1⋅⋅⋅bm]]x_1 \begin{bmatrix} a_{11} \\ \cdot \\ \cdot \\ \cdot \\ a_{m1} \end{bmatrix} + x_2\begin{bmatrix} a_{12} \\ \cdot \\ \cdot \\ \cdot \\ a_{m2} \end{bmatrix} + \cdots + x_n \begin{bmatrix} a_{1n} \\ \cdot \\ \cdot \\ \cdot \\ a_{mn} \end{bmatrix} = [\begin{bmatrix} b_{1} \\ \cdot \\ \cdot \\ \cdot \\ b_{m} \end{bmatrix}] 또한 이를 matrix 형태로 나타낼 수 있다. [a11⋯a1n⋮⋮ am1⋯amn][x1⋅⋅⋅xn]\begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots && \vdots \ \\ a_{m1} &\cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_{1} \\ \cdot \\ \cdot \\ \cdot \\ x_{n} \end{bmatrix}