Vector란

서로 더하거나 scalar를 곱해도 vector이다. 이를 더욱 수학적으로 나타내보자.

Group

vector를 표현하기 위해서 group이라는 개념이 필요하다.

group이란, set과 operation으로 이루어진 개념이다. 아래와 같이 set과 operation으로 group을 정의할 수 있다.

  • Set: $g$
  • Operations: $\otimes$
G=(g,⊗)G = (g, \otimes)

그리고 group은 다음과 같은 조건이 성립되어야 한다.

  • Closure of $g$ under $\otimes$: ∀x,y∈g:x⊗y∈g\forall x, y \in g: x \otimes y \in g

  • Associativity: ∀x,y,z∈g:(x⊗y)⊗z=x⊗(y⊗z)\forall x, y, z \in g: (x \otimes y) \otimes z = x \otimes (y \otimes z)

  • Neutral Element: ∃e∈g,x∈g:x⊗e=x,e⊗x=x\exists e \in g, x \in g: x \otimes e = x, e \otimes x = x

  • Inverse Element:

    • $e$: neutral element
    ∀x,∃y:x⊗y=e,y⊗y=e\forall x, \exists y: x \otimes y = e, y \otimes y = e

Abelian group

  • Commutative: ∀x,y∈g:x⊗y=y⊗x\forall x, y \in g: x \otimes y = y \otimes x 위와 같은 조건을 추가적으로 만족하면 abelian group이라고 정의한다.

다음과 같은 예시를 생각해보자.

  • set: regular matrices(invertible)
  • Operation: matrix multiplication

set과 operation은 group의 조건을 만족한다. 하지만, commutative한 성격은 만족하지 못하므로, abelian group은 아니다. ∀x,y∈Rn∗m:xy≠yx\forall x,y \in R^{n * m} : xy \neq yx

Vector space

group의 개념에 대해서 살펴봤으니, 이제 vector space에 대한 정의를 해볼 것이다. 우선 operation에 대해서 먼저 언급하고 가겠다.

operation은 크게 두 가지로 볼 수 있다.

  • 같은 집합내에서 정의되는 inner operation
  • 다른 집합간의 정의되는 outer operation

vector로 예를 들면, vector끼리 더하는 것은 inner operation이고 scalar를 곱하는 것은 outer operation이다.

이제 vector space를 정의해보자. +:V×V→V⋅:V×R→V+: \mathcal{V} \times \mathcal{V} \rightarrow \mathcal{V} \\ \cdot:\mathcal{V} \times R \rightarrow \mathcal{V}

V=(V,+,⋅)V = (\mathcal{V}, +, \cdot )

그리고 vector space는 다음과 같은 성질을 가진다.

  1. $V = (\mathcal{V}, + )$ 는 abelian group이다.

  2. Distributivity ∀λ∈R,x,y∈V:λ(x+y)=λx+λy\forall \lambda \in R, x, y \in V: \lambda (x + y) = \lambda x + \lambda y

    ∀λ,ψ∈R,x∈V:(λ+ψ)x=λx+ψx\forall \lambda, \psi \in R, x \in V: (\lambda + \psi) x = \lambda x + \psi x

  3. Associativity(outer operation) ∀λ,ψ∈R,x∈V:(λ⋅ψ)⋅x=λ⋅(ψ⋅x)\forall \lambda, \psi \in R, x \in V: (\lambda \cdot \psi) \cdot x = \lambda \cdot (\psi \cdot x)

  4. Neutral element with respect to the outer operation ∀x∈V:1⋅x=x\forall x \in V: 1 \cdot x = x

REMARK

vector multiplication은 vector space에서 정의하지 않는다.

Vector subspace

$V = (\mathcal{V}, +, \cdot )$ vector space가 주어졌을 때, 다음과 같은 조건을 만족하면, $V$의 vector subspace라고 정의한다.

$U \subset V$가 vector space이며, operation $+, \cdot$이 $U + U, R \cdot U$에 한정되어 있다면, $V$의 vector subspace라고 한다.

다음과 같은 케이스들을 생각해보자.

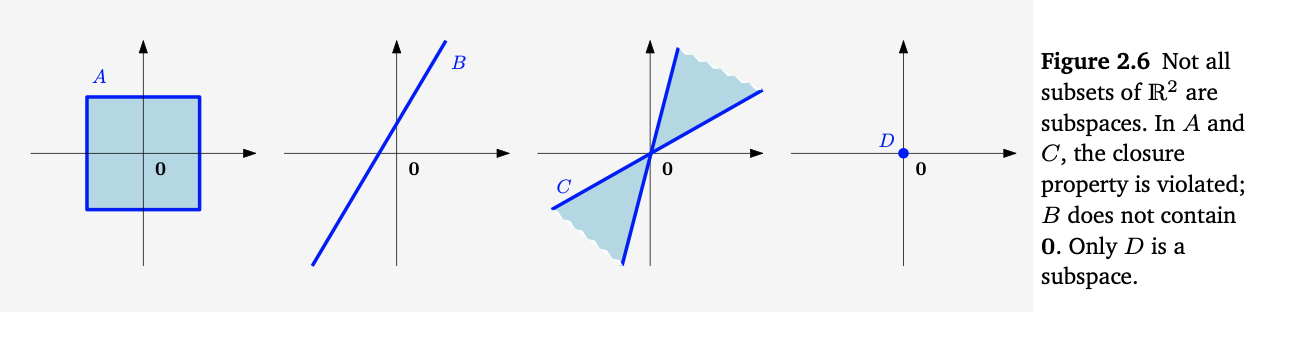
image-20200829215134170

A, C는 inner operation, outer operation 모두에 대해서 closure 조건을 충족하지 못한다. 반면에 B는 0을 포함하지 못하므로, outer operation에 대해서 closure 조건을 충족하지 못한다. D는 모든 조건을 만족하므로 V의 subspace이다.

Linear equation system에 대해서 생각해보자. Ax=0Ax = 0 solution set $x = [x_0, \cdots, x_n] \in R^n$은 vector subspace이다.

  • $X$: solution set
A⋅(λx)=0A \cdot (\lambda x ) = 0 ∀x1,x2∈X,Ax1+Ax2=0\forall x_1, x_2 \in X, Ax_1 + Ax_2 = 0

반면에, 다음과 같은 linear equation의 solution set은 vector subspace가 아니다. Ax=a≠0Ax = a \neq 0

A⋅(λx)≠aA\cdot (\lambda x) \neq a ∀x1,x2∈X,Ax1+Ax2=2a\forall x_1, x_2 \in X, Ax_1 + Ax_2 = 2a