이번 chapter의 요약 마인드맵입니다.

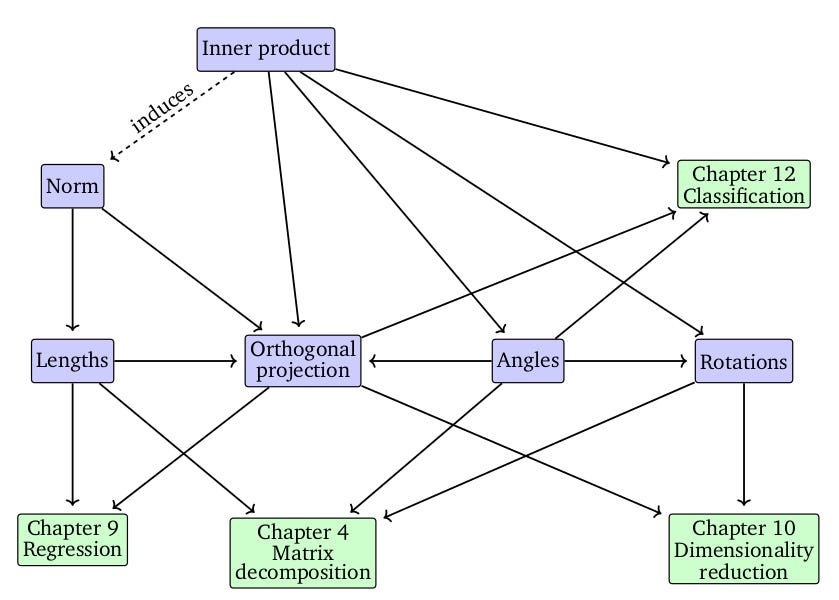
Norm

어떤 vector space에 대한 norm은 다음과 같은 function이다. ∥⋅∥:V→R,x→∥x∥∈R\lVert \cdot \rVert: V \rightarrow R, x \rightarrow \lVert x \rVert \in R 이는 직관적으로 vector x에 length를 부여한다고 해석할 수 있다.

그리고 norm은 아래와 같은 특성을 가진다.

  • $x, y \in V$
  • $\lambda \in R$

Absoultely Homogeneous ∥λx∥=∣λ∣∥x∥\rVert \lambda x\rVert = \rvert \lambda \rvert \rVert x \rVert Triangle inequality ∥x+y∥≤∥x∥+∥y∥\rVert x + y \rVert \le \rVert x \rVert + \rVert y \rVert

Positive Definite ∥x∥≥0,∥x∥=0  ⟺  x=0\rVert x \rVert \ge 0, \rVert x \rVert = 0 \iff x =0

Norm의 종류들

  • Manhattan Norm

  • Euclidean Norm

  • Mahalanobis Norm

    • $S$: covariance matrix

  • $u$: mean vector