High Dimensional Data

고차원의 데이터를 분석하거나 시각화하는 것은 힘든 일이다. 따라서 고차원의 데이터를 다룰 때, 종종 고차원의 데이터를 저차원으로 projection 시켜서 작업을 한다. 하지만, 이렇게 저차원으로의 projection은 필연적으로 정보 손실을 가져오게 되는데, 이때, 정보손실을 최소화하면서 projection을 시키는 것이 중요하다.

Projection

  • $V$: vector space
  • $U \subset V$: vector subspace of V
  • $\pi$: linear mapping
π:V→U,π∘π=π\pi: V \rightarrow U,\\\pi \circ \pi = \pi

linear mapping은 matrix형태로 나타낼 수 있기 때문에, projection은 다음과 같이 표현할 수 있다. PπP_{\pi} 그리고 projection matrix는 다음과 같은 조건을 만족해야한다. Pπ2=PπP_{\pi}^2 = P_{\pi}

Orthogonal Projection: One Dimensional Subspace

이 책에서는 주로 orthogonal projection에 대해서 다룬다. 이유에 대해서 생각해보면, compression loss를 최소화할 수 있는 방법이기 때문!

우선, 1차원의 vector subspace에 projection 시키는 문제에 대해서 정리해볼 계획이다.

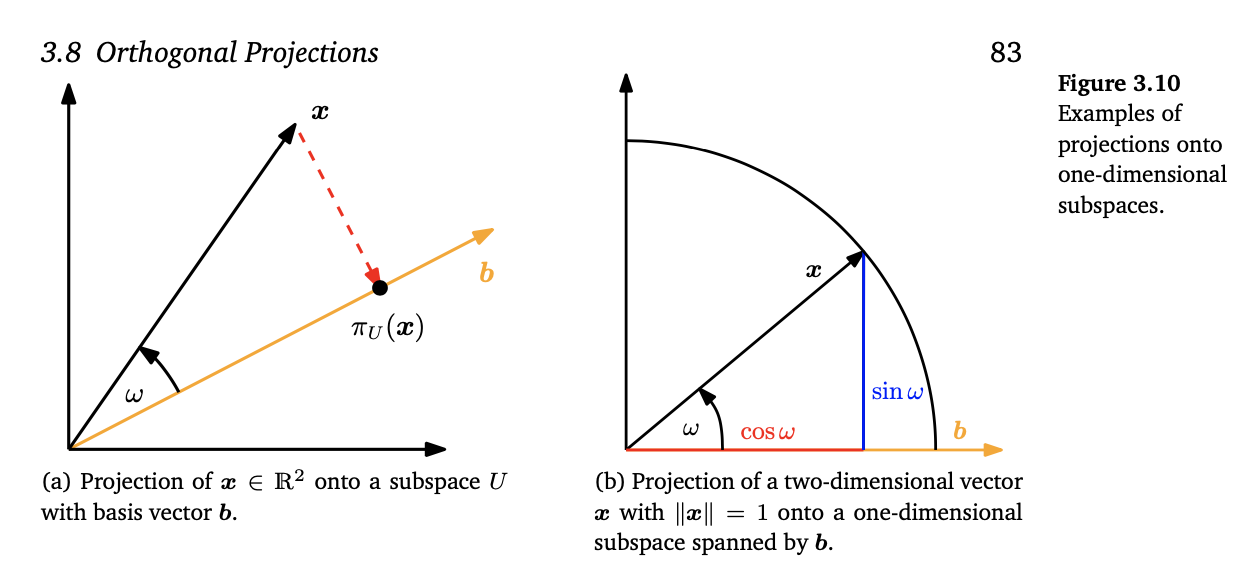
image-20201024183854145

subspace $U \in V$는 위의 (a)에서 노란색 라인을 의미한다. 이 때, basis는 $b \in U$이다. 그리고 $x \in V$는 이제 앞으로 subspace U에 projection 할 것이고, 이를 $\pi_U{x}$라고 표현한다. ($V \in R^2$)

  • $\Pi_U{x}$ 는 $x$와 vector subspace U내에서 가장 가까운 점이다. 가장 가깝다라는 것의 수학적인 의미는 $\rVert x - \pi_U(x)\rVert$가 가장 작다는 뜻이며, 이는 distance vector $ x - \pi_U(x)$가 $U$와 orthogonal하다는 것이다.

  • <x−πU(x),b>=0< x - \pi_U(x), b> = 0

  • $\pi_U(x)$는 U내에 존재해야한다.

    • πU(x)=λb\pi_U(x) = \lambda b

앞서서 orthogonal projection한 결과가 어떤 특징을 가지는지 살펴봤다. 이제는 어떤식으로 구하는지 살펴보겠다.

앞의 식을 다음과 같이 변경할 수 있다. <x−πU(x),b>=0  ⟺  <x−λb,b>=0< x - \pi_U(x), b> = 0 \iff <x - \lambda b, b> = 0

<x,b>−<λb,b>=0  ⟺  λ=<x,b><b,b><x, b> - <\lambda b,b > = 0 \iff \lambda = \frac{<x, b>}{<b, b>} λ=bTxbTb\lambda = \frac{b^T x}{b^T b}

$\lambda$에 대해서 구했으니, 이를 $\pi_U$에 대해서 적용해보겠다. πU(x)=λb=bTx∥b∥2b\pi_U(x) = \lambda b =\frac{b^T x}{\rVert b \rVert^2} b $\pi_U(x) = \lambda b $은 직관적으로는 projection 함수의 결과가 U에서의 coordinate라는 것을 알 수 있다. ∥πU(x)∥=∥λb∥=∥λ∥∥b∥\rVert \pi_U(x)\rVert = \rVert \lambda b \rVert = \rVert \lambda \rVert \rVert b \rVert

그리고 이를 cosine으로 나타내면 다음과 같다. (b) 참고 ∥πU(x)∥=∥bTx∥∥b∥2∥b∥=∣cosw∣∥x∥\rVert \pi_U(x)\rVert = \frac{ \rVert b^T x \rVert}{\rVert b \rVert^2} \rVert b\rVert =\rvert cos w \rvert \rVert x\rVert

Pπ=bTx∥b∥2P_{\pi} = \frac{b^T x}{\rVert b \rVert^2}

Orthogonal Projection: General Subspace

이제 general한 orthogonal projection에 대해서 알아볼 것이다. 이제 projection 되는 공간은 $U \in R^k, k > 1$이다.

  • $B = [b_1, b_2, \cdots, b_k\ ] \in R^{nk}$
  • $\lambda = [\lambda_1, \lambda_2, \cdots, \lambda_k] \in R^k$
πU(x)=∑i=1kλibi=Bλ\pi_U(x) = \sum_{i=1}^k \lambda_i b_i = B\lambda <b1,x−πU(x)>=b1T(x−πU(x))=0<b_1, x - \pi_U(x)> = b_1^T( x - \pi_U(x)) = 0 <b2,x−πU(x)>=b2T(x−πU(x))=0<b_2, x - \pi_U(x)> = b_2^T( x - \pi_U(x)) = 0 ⋮\vdots <bk,x−πU(x)>=bkT(x−πU(x))=0<b_k, x - \pi_U(x)> = b_k^T( x - \pi_U(x)) = 0

이를 조금 matrix로 표현하면 다음과 같다. b1T(x−Bλ)=0b_1^T (x - B\lambda) = 0

⋮\vdots bkT(x−Bλ)=0b_k^T (x - B\lambda) = 0

[b1⋮bk][x−Bλ]=0  ⟺  BT(x−Bλ)=0  ⟺  BTBλ=BTx\begin{bmatrix} b_1 \\ \vdots \\ b_k \end{bmatrix} \begin{bmatrix} x - B\lambda \end{bmatrix} = 0 \iff B^T(x - B\lambda) = 0 \\ \iff B^TB \lambda = B^T x 위에서 마지막 식은 normal equatioin*이라고 한다. 또한 B는 basis로 이루어진 matrix이기 때문에 $B^T B$는 regular하며, invertable하다. λ=(BTB)−1BTx\lambda = (B^TB)^{-1}B^T x 이제 다시 projection을 정리해보겠다. πU(x)=Bλ=B(BTB)−1BTx\pi_U(x) = B \lambda = B(B^TB)^{-1}B^T x 이를 바탕으로 projection matrix $P_{\pi}$를 구해보면 다음과 같다. Pπ=B(BTB)−1BTP_{\pi} = B(B^TB)^{-1}B^T 직관적으로 projection을 하게 되면, 기존의 m차원의 공간의 vector를 n차원을 vector로 표현할 수 있게 된다. 이러한 점을 활용하여, linear equation $Ax = b$의 해가 없을 때, 근사하여 구할 수 있다.

$Ax = b$의 해가 없다는 것은 $b$가 A의 basis로 span되는 공간에 없다는 것이다. 하지만, A의 span되는 공간에서 b와 가장 가까운 점을 구할 수 있는데, 이 해를 least square solution이라고 한다.

Remark: orthonormal basis

Subspace U의 basis가 orthonormal basis라면, πU(x)=B(BTB)−1BTx=BBTx\pi_U(x) = B(B^TB)^{-1}B^T x = B B^T x

  • $(B^TB) ^(-1) = I$

따라서 λ=BTx\lambda = B^T x 불필요하게 inverse를 구할 필요가 없다.

Gram-Schmidt Orthogonalization

Gram-schmidt orthogonalization은 어떤 basis는 orthogonal/orthonormal basis로 바꿔준다. 또한 orthogonal basis는 항상 존재하며, span되는 공간은 변하지 않는다.

다음과 같은 과정을 통해서 gram-schmidt orthogonalization이 진행된다.

  • basis: $[b_1, b_2, \cdost, b_n]$
  • orthogonal basis: $u_1, u_2, \cdots, u_n$
u1=b1u_1 = b_1 uk=bk−πspan[u1,⋯ ,uk−1](bk)u_k = b_k - \pi_{\text{span}[u_1, \cdots, u_{k-1}]}(b_k)

Projection onto Affine Space

아직까지 vector subspace상에서의 projection을 다뤘다. 그럼 affine space상으로의 projection은 어떻게 진행될지 살펴보겠다.

위의 이미지에서 (a)는 affine space $L = x_0 + U$과 vector subspace U의 basis b1, b2가 나타나있다. 여기서 x vector의 L space상으로의 projection은 다음과 같이 나타낼 수 있다. πL(x)∈L\pi_L(x) \in L 위의 문제를 풀기 위해서, 기존의 vector subspace상에서의 projection을 활용한다. 이를 위해서 $x - x_0$을 vector subspace U에 projection시킨다. πU(x−x0)∈U\pi_U(x-x_0) \in U 이 것의 의미는 U와 L사이의 관계를 생각해보면 이해하기 쉽다. L은 U로 부터 $x_0$만큼 이동한 공간이다. 따라서 x가 L에 projection되는 위치는 $x - x_0$이 U에 projection되는 위치에 x_0을 더한 것과 같다. L=x0+UL = x_0 + U 따라서, πL(x)=x0+πU(x−x0)∈L\pi_L(x) = x_0 + \pi_U(x-x_0) \in L Remark d(x,L)=d(x−x0,L)d(x, L) = d(x - x_0, L)