Dropout as Bayesian Approximation 정리글

Problem

일반적으로 Bayesain model은 model의 uncertainty를 측정할 수 있다는 장점이 있지만, computation cost가 너무 커서 사용하기 힘들다는 문제를 가지고 있다. 이런 문제점을 해결하기 위해서 이 논문에서는 Dropout을 사용한 딥러닝 모델이 결국은 gaussian porcess에서의 bayesain inference를 근사한 것이라는 증명을 할 것이다.

  • Bayesian learning for neural networks

    infinite-wide neural network에 distribution을 가정하면, 결국 gaussian process를 approxiation하는 것이다. 하지만 finite-wide neural network에서는 증명되지 않았다.

    추가적으로 finite-wide neural network상에서 연구되었다. BNN 조건에서 overfitting문제에 견고했지만, computation cost 높다는 문제가 있었다.

  • variational inference

    BNN에서 variational inference가 적용되었다. 하지만, 부분적인 성과만 있었다.

  • sampling-based variational inference

    위의 VI를 개선하기 위해서 sampling 기반의 방법론이 등장하였다. 이 방법론은 dropout만큼 성공적이였으나 computation cost가 매우 높았다. uncertainty를 측정하기 위해서 parameter가 기존의 방법론 대비 두 배가 필요했다. 이는 분포를 정의하기 위해서 평균값과 분산값을 정의해야 되기 때문이다. 게다가 수렴하는 시간도 오래걸렸으며, 기존의 방법론 대비 효과적이지도 않았다.

Dropout as a Bayesian Approximation

이 section에서는 Dropout이 결국에는 Deep gaussian process를 근사한다는 것을 수학적으로 증명할 것이다. 특히, 어떠한 가정도 없이 증명할 수 있으며, 어떤 network에도 적용가능하다는 장점을 가지고 있다.

Dropout objective는 approximation distribution과 deep gaussian process의 posterior간의 Kl-divergence를 감소시킨다.

우선 Dropout objective를 확인해보자. ( add regularization)

Ldropout=1N∑i=1NE(yi,y^i)+λ∑i=1N(∥Wi∥22+∥b∥22)\mathcal{L}_{dropout} = \frac{1}{N}\sum_{i=1}^N E(y_i, \hat{y}_i) + \lambda\sum_{i=1}^N (\rVert W_i \rVert_2 ^ 2+ \rVert b \rVert_2 ^ 2)

dropout은 결국 모든 input point와 각 layer의 모든 network에 binary distribution을 적용한 것으로 해석할 수있다. 참고로 output에는 적용하지 않는다. 이는 아래의 이미지 처럼 적용될 수 있다.

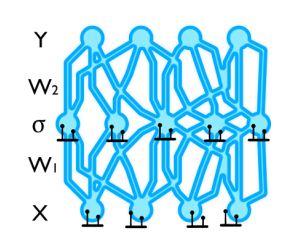
GP 모델에서 predictive probability는 아래와 같이 전개된다. ($x^*$ is unseen)

p(y∣x∗,X,Y)=∫p(y∣x∗,w)p(w∣X,Y)dwp(y\mid x^*, X, Y) = \int p(y\mid x^*, w) p(w\mid X, Y) dw p(y∣x,w)=N(y;y^(x,w),τ−1ID)p(y\mid x, w) = \mathcal{N}(y; \hat{y}(x, w), \tau^{-1}I_D) y^(x,w={W1,⋯ ,WL})=1KLWLσ(⋯1K1W2σ(W1x+m1)⋯ )\hat{y}(x, w= \{ W_1, \cdots, W_L\}) = \sqrt\frac{1}{K_L}W_L\sigma( \cdots \sqrt\frac{1}{K_1}W_2 \sigma(W_1x + m_1) \cdots)

여기서 posterior $p(w\ mid X, Y)$가 untractable한데 이를 해결하기 위해서 variational inference를 사용하며, simple distribution으로 $q(w)$를 가정한다. 이때 $q(w)$는 matrix형태를 가지고 있으며 random하게 0으로 값이 지정된다. (여기서 $K$ 는 matrix dimension을 의미한다. $W_i$ 의 dim은 $K_i * K_{i-1}$)

Wi=Mi⋅diag([zi,j]j=1Ki)W_i = M_i \cdot diag([z_{i, j}]_{j=1}^{K_i}) Zi,j=Bernoulli(pi) for i=1,⋯ ,L, j=1,⋯ ,Ki−1Z_{i, j} = Bernoulli(p_i) \ for \ i = 1, \cdots, L, \ j= 1, \cdots, K_{i-1}

여기서 $z_{i, j}$가 0이라면, layer $i - 1$ 의 unit $j$가 drop된다는 것을 의미한다. 위의 이미지에서는 layer에 dropout을 설정한 것을 시각화 한것이라면 위의 수식은 parameter자체에 dropout을 걸었다는 차이가 있다. (그리고 BNN을 적용하기 위해서는 위의 수식처럼 parameter 자체에 dropout을 설정하는 것이 타당하다고 생각한다.)

variational distribution $q(w)$는 highly multi modal한 특징을 가지고 있다. 왜냐하면, 각 layer에 대한 Bernoulli distribution의 output값이 layer의 크기 만큼 나와야 하기 때문이다.

$q(w)$를 바탕으로 objective를 도출하면 아래와 같다. (lower bound: variational inference 참고)

−∫q(w)log⁡p(Y∣X,w)dw+KL(q(w)∥p(w)).- \int q(w) \log p(Y \mid X, w) dw +KL(q(w) \rVert p(w)).
  • $p(w)$ 는 prior distribution을 의미한다.

첫번째 term $- \int q(w) \log p(Y\mid X, w) dw$은 아래처럼 바꿀 수 있다.

−∫q(w)log⁡p(Y∣X,w)dw≈−∑n=1N∫q(w)log⁡p(yn∣xn,w)dw- \int q(w) \log p(Y\mid X, w) dw \approx- \sum_{n=1} ^N \int q(w) \log p(y_n \mid x_n, w) dw

두번째 term $ KL(q(w) \rVert p(w))$에서는 아래와 같은 식을 얻을 수 있다.

∑i=1L(pil22∥Mi∥22+l22∥mi∥22)\sum_{i=1}^ L(\frac{p_il^2}{2}\rVert M_i\rVert_2^2 + \frac{l^2}{2}\rVert m_i \rVert_2^2)
  • $p_i$ bernoulli 분포의 확률값
  • $l$ 은 prior length scale 값: appendix section 4.2
    • prior distribution에 대한 가정

appendix section 4.2 KL(q(w)∥p(w))≈∑i=1Lpi2(uiTui+tr(Σi)−K(1+log⁡2π)−log⁡∣Σi∣−C)KL(q(w) \rVert p(w)) \approx \sum_{i=1}^L \frac{p_i}{2}(u_i^Tu_i + tr(\Sigma_i) - K(1 + \log2\pi) - \log\rvert\Sigma_i \rvert - C)

model precision $\tau$를 고려하면, 아래와 같이 scale한 값이 도출된다.

LGP−MC∝1N∑i=1N−log⁡p(yn∣xn,wn^)τ+∑i=1L(pil22τN∥Mi∥22+l22τN∥mi∥22)\mathcal{L}_{GP-MC} \propto \frac {1}{N}\sum_{i=1}^N\frac{- \log p (y_n \mid x_n, \hat{w_n})}{\tau} + \sum_{i=1}^{L}(\frac{p_i l^2}{2\tau N}\rVert M_i\rVert_2^2 + \frac{l^2}{2\tau N}\rVert m_i \rVert_2^2)

여기서 $\tau$와 length-scale $l$은 hyperparameter이다. lengh-scale은 function frequency를 가정하는 것으로 만약 $l$을 강하게 준다면, regularization 효과는 더 강해진다.

λ1=l2p12Nτ\lambda_1 = \frac{l^2 p_1}{2N\tau} τ=l2p12Nλ1\tau = \frac{l^2 p_1}{2N \lambda_1}
  • short length scale $l$ (high frequency data) + high precision $\tau$(small observation noise) result in small weight-decay $\lambda$ : 모델이 데이터에 더 잘 적합하게 된다.
  • long length scale $l$ (low frequency data) + low precision $\tau$ (large observation noise) result in large weight-decay

Obtaining Model Uncertainty

predictive distributioin은 아래와 같이 주어진다.

q(y∗∣x∗)=∫p(y∗∣x∗,w)q(w)dwq(y^*\mid x^*) = \int p(y^*\mid x^*, w) q(w) dw
  • $w = { W_i}_{i=1} ^ L$
  • unseen input data: $x^*$
  • prediction from unseen input data: $y^*$

dropout을 이용하여, uncertainty를 estimate를 하기 위해서는 bernoulli distribution ${z_1^t, \cdots, z_L^t}_{t=1}^T$를 sampling해주면 된다. 이 식에서는 T번의 sampling을 진행한 것이다.

sampling한 분포를 바탕으로 predictive mean값을 근사할 수 있다. 이를 MC-dropout이라고 부른다.

Eq(y∗∣x∗)(y∗)=1T∑i=1Ty^∗(x∗,W1t,⋯ ,WLt)E_{q(y^* \mid x^*)}(y^*) = \frac{1}{T}\sum_{i=1}^T \hat{y}^*(x^*, W_1^t, \cdots, W_L^t)

다음은 raw moment를 근사하는 과정이다.

Eq(y∗∣x∗)((y∗)Ty∗)≈τ−1ID+1T∑i=1Ty^∗(x∗,W1t,⋯ ,WLt)Ty^∗(x∗,W1t,⋯ ,WLt)E_{q(y^* \mid x^*)}((y^*) ^T y^*) \approx \tau^{-1}I_D +\frac{1}{T}\sum_{i=1}^T \hat{y}^*(x^*, W_1^t, \cdots, W_L^t) ^ T \hat{y}^*(x^*, W_1^t, \cdots, W_L^t)

predictive variance는 다음과 같이 도출된다.

Varq(y∗∣x∗)(y∗)≈τ−1ID+1T∑i=1Ty^∗(x∗,W1t,⋯ ,WLt)Ty^∗(x∗,W1t,⋯ ,WLt)−Eq(y∗∣x∗)(y∗)TEq(y∗∣x∗)(y∗)Var_{q(y^* \mid x^*)}(y^*) \approx \tau^{-1}I_D + \frac{1}{T}\sum_{i=1}^T \hat{y}^*(x^*, W_1^t, \cdots, W_L^t) ^ T \hat{y}^*(x^*, W_1^t, \cdots, W_L^t) -E_{q(y^* \mid x^*)}(y^*) ^T E_{q(y^* \mid x^*)}(y^*)

참고로 $y^$는 row vector를 의미하며 $ \hat{y}^(x^, W_1^t, \cdots, W_L^t) ^ T \hat{y}^(x^*, W_1^t, \cdots, W_L^t)$ 연산은 outer product이다.

weight-decay 값 $\lambda$와 length scale $l$이 주어지면 아래의 식으로 model precision $\tau$ 를 도출할 수 있다.

τ=l2p12Nλ1\tau = \frac{l^2 p_1}{2N \lambda_1}

regression task에서 다음과 같이 predictive log-likelihood를 monte-carlo integration을 통해서 근사할 수 있다. 이를 통해서 model이 mean과 얼마나 일치하는지 uncertainty가 어떤지 알 수 있다.

with $w_t \sim q(w)$ \begin{align} \log p(y^* \mid x^*, X, Y) &= \log \int p(y^* \mid x^*, w) p(w \midX, Y) dw\\ & \approx \log \int p(y^* \mid x^*, w) q(w) dw \\ &\approx \log\frac{1}{T} \sum_{t=1}^{T} p(y^* \mid x^*, w_t) \end{align}

At regression task,

log⁡p(y∗∣x∗,X,Y)≈logsumexp(−12τ∥y−y^∥2)−log⁡T−122π−12log⁡τ−1\log p(y^* \mid x^*, X, Y) \approx \mathrm{logsumexp} ( -\frac{1}{2}\tau\rVert y - \hat{y}\rVert^2) -\log T - \frac{1}{2}2\pi - \frac{1}{2}\log \tau ^{-1}
  • $y$ : predictive mean
  • $\hat{y}$ : sample

predictive distribution $q(y^* \mid x^*)$은 highly multi modal이기 때문에 그 특성을 정확히 알 수 없다. 이는 weight element에 bi-modal한 distribution을 설정하였고 이들의 joint distribution은 multi modal이기 때문이다.

하지만, 구현하기 매우 싶다. dropout을 수정하지 않고 사용하며, samples을 모아서 uncertainty를 측정할 수 있다. 또한 forward pass는 기존의 standard 한 모델과 차이가 나지 않는다.

Example code: image segmentaton

아래는 test과정에서 predictive mean를 구하는 method의 예시이다. 주목할 점은 dropout을 낀채로 sampling을 진행해야 한다는 것이다.

def test_epistemic(model, test_loader, criterion, test_trials=20, epoch=1):
    """Epistemic model Test
    Please turn on Dropout!
    model: pytorch model
    test_loader: test data loader
    crieterion: loss_fucntion
    Return
        test_loss, test_error
    """
    model.train()  # train mode: turn on dropout
    test_loss = 0
    test_error = 0
    for data, target in test_loader:
        if list(data.size())[0] != batch_size:
            break
        data = Variable(data.cuda(), volatile=True)
        target = Variable(target.cuda())
        outputs = model(data)[0].data
        for i in range(test_trials - 1): # sampling
            outputs += model(data)[0].data
        output = outputs / test_trials  # predictive mean
        pred = get_predictions(output)
        test_loss += criterion(output, target).data
        test_error += error(pred, target.data.cpu())
        torch.cuda.empty_cache()
    test_loss /= len(test_loader)
    test_error /= len(test_loader)
    torch.cuda.empty_cache()
    return test_loss, test_error

다음은 predictive variance를 구하는 과정이다.

def get_epistemic(outputs, predictive_mean, test_trials=20):
    result = torch.tensor(
        np.zeros((batch_size, img_shape[0], img_shape[1]), dtype=np.float32)
    ).cuda()
    target_sq = torch.einsum("bchw,bchw->bhw", [predictive_mean, predictive_mean]).data
    for i in range(test_trials):
        output_sq = torch.einsum(
            "bchw,bchw->bhw", [outputs[i], outputs[i]]
        ).data
        result += output_sq - target_sq
    result /= test_trials
    return result

Reference

  • https://arxiv.org/abs/1506.02142