Partial Differentiation and Gradients

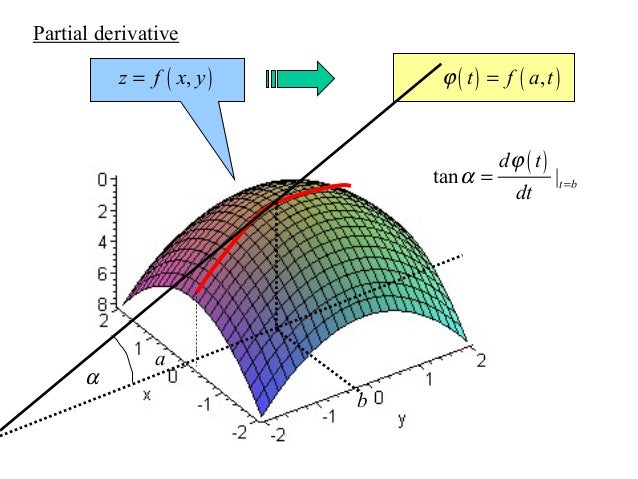
Differentiation에서는 input $x \in R$는 scalar 값이었다. Partial Differentiation은 input $x \in R^n$이 vector 형태이며 앞의 differentiation보다 조금 더 일반화된 미분에 대해서 알아볼 것이다.

Definition 5.5: Partial Derivative

Function $f: R^n \rightarrow R$이 있다고 했을 때, partial derivertive는 다음과 같이 정의된다.

  • $x \searrow f(x), x \in R^n$: n개의 variable, $x_1, \cdots, x_n$
∂f∂x1=lim⁡h→0f(x1+h,x2,⋯ ,xn)−f(x)h∂f∂x2=lim⁡h→0f(x1,x2+h,⋯ ,xn)−f(x)h...∂f∂xn=lim⁡h→0f(x1,x2,⋯ ,xn+h)−f(x)h\frac{\partial f}{\partial x_1} = \lim_{h \rightarrow 0} \frac{f(x_1 + h, x_2, \cdots, x_n) - f(x)}{h} \\ \frac{\partial f}{\partial x_2} = \lim_{h \rightarrow 0} \frac{f(x_1, x_2 + h, \cdots, x_n) - f(x)}{h} \\ . \\ . \\ . \\ \frac{\partial f}{\partial x_n} = \lim_{h \rightarrow 0} \frac{f(x_1, x_2, \cdots, x_n + h) - f(x)}{h}

그리고, 위의 값들을 row vector의 형태로 모을 수 있다. 그리고 이 row vector를 jcobian 혹은 f의 gradient라고 한다. ∇xf=grad f=dfdx=[∂f(x)∂x1,∂f(x)∂x2,⋯ ,∂f(x)∂xn]\nabla_x f = grad \ f = \frac{df}{dx} = [\frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, \cdots, \frac{\partial f(x)}{\partial x_n}]

Remark

일반적으로 gradient는 column vector의 형태가 아닌 row vector의 형태로 나타낸다. 여기에는 두 가지 이유가 있는데 다음과 같다.

  • $f: R^n \rightarrow R^m$의 함수꼴의 gradient를 구할 때 자연스럽게 matrix 형태의 jacobian이 나온다.
  • multivariate chain rule을 적용할 때, 편리하다.

Basic Rules of Partial Differentiation

  • product rule ∂(f(x)g(x))∂x=∂f∂x(g(x))+∂g∂x(f(x))\frac{\partial (f(x)g(x)) }{\partial x} = \frac{\partial f }{\partial x}(g(x)) +\frac{\partial g }{\partial x}(f(x))

  • sum rule ∂(f(x)+g(x))∂x=∂f(x)∂x+∂g(x))∂x\frac{\partial (f(x) + g(x)) }{\partial x} = \frac{\partial f(x) }{\partial x} + \frac{\partial g(x)) }{\partial x}

  • chain rule ∂(g∘f(x))∂x=∂g(f(x))∂x=∂f(x)∂x∂g(f(x))∂f(x)\frac{\partial (g \circ f(x))}{\partial x} = \frac{\partial g(f(x))}{\partial x} = \frac{ \partial f(x)}{\partial x} \frac{\partial g(f(x))}{\partial f(x)}

Chain Rule

chain rule은 deep learning backpropagation 과정에서 핵심이 되는 부분이다. 이번 장에서는 조금 더 자세히 살펴보겠다.

  • $f: R^2 \rightarrow R$: two variable $x_1, x_2$
  • $x_1(t), x_2(t)$: $x_1, x_2$도 t에 대한 함수이다.
dfdt=[∂f∂x1,∂f∂x2][∂x1∂t∂x2∂t]=∂f∂x1∂x1∂t+∂f∂x2∂x2∂t\frac{df}{dt} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{ \partial x_2}] \begin{bmatrix} \frac{\partial x_1}{ \partial t} \\ \frac{\partial x_2}{ \partial t} \end{bmatrix} = \frac{\partial f}{\partial x_1} \frac{\partial x_1}{ \partial t} + \frac{\partial f}{ \partial x_2}\frac{\partial x_2}{ \partial t}

그렇다면, 이제 다음과 같은 수식으로 확장해보자.

  • $x_1(s, t), x_2(s, t)$: $x_1, x_2$도 s, t에 대한 함수이다.

각 s, t에 대해서 partial derivative를 구하게 되면 아래와 같다. dfdt=∂f∂x1∂x1∂t+∂f∂x2∂x2∂tdfds=∂f∂x1∂x1∂t+∂f∂x2∂x2∂s\frac{df}{dt} = \frac{\partial f}{\partial x_1} \frac{\partial x_1}{ \partial t} + \frac{\partial f}{ \partial x_2}\frac{\partial x_2}{ \partial t} \\ \frac{df}{ds} = \frac{\partial f}{\partial x_1} \frac{\partial x_1}{ \partial t} + \frac{\partial f}{ \partial x_2}\frac{\partial x_2}{ \partial s} 그리고 이를 matrix 형태로 나타내면 아래와 같다. dfd(s,t)=[∂f∂x1,∂f∂x2][∂x1∂s∂x1∂t∂x2∂s∂x2∂t]\frac{df}{d(s, t)} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{ \partial x_2}] \begin{bmatrix} \frac{\partial x_1}{ \partial s} & \frac{\partial x_1}{ \partial t}\\ \frac{\partial x_2}{ \partial s} & \frac{\partial x_2}{ \partial t} \end{bmatrix}