Backpropagation and Automatic Backpropagation

Gradient in A Deep Network

e.g. multi level function composition

  • $x$: input
  • $y$: observation, class label
  • $f_i$: poses own parameters
y=(fK∘fK−1⋯∘f1)(x)y = (f_K \circ f_{K-1} \cdots \circ f_1)(x)

위의 수식을 아래처럼 도식으로 나타내면 아래와 같다.

  • $A_i, b_i$: weight parameter, bias parameter

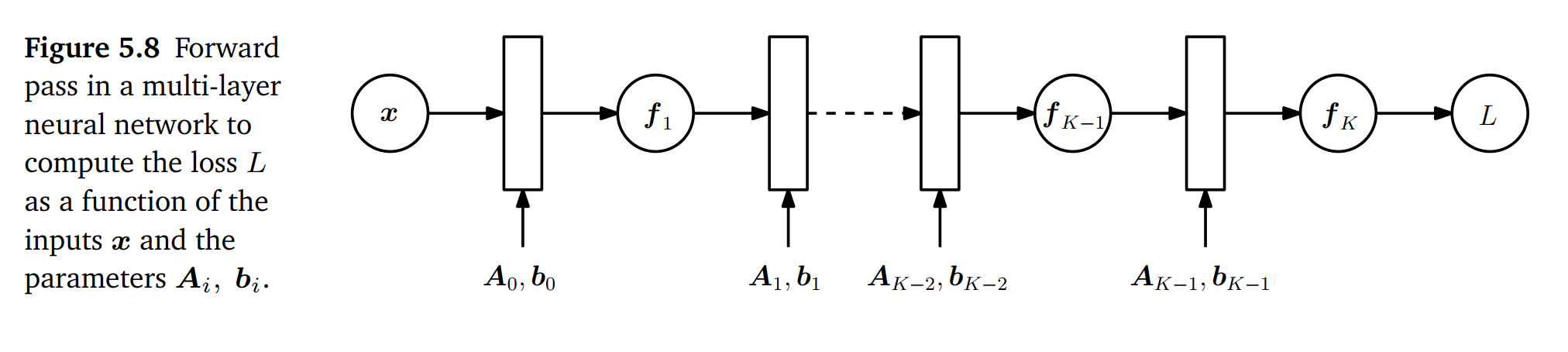f0=xfi=σi(Ai−1fi−1+bi−1), i=1,⋯ ,Kf_0 = x \\ f_i = \sigma_i(A_{i-1}f_{i-1} + b_{i-1}), \text{ $i = 1, \cdots, K$}

loss function을 squared loss를 사용한다면, 아래와 같이 전개할 수 있다.

  • $\theta_i ={A_i, b_i }$
L(θ)=∥y−fK(θ,x)∥22L(\theta) = \rVert y - f_K(\theta, x)\rVert^2_2

이를 바탕으로 각 레이어 마다 발생하는 partial derivertive를 구하게 되면 다음과 같다. 그리고 전개해보면, 전체 레이어 대상으로 Backpropagation을 진행할 때, 중복되는 연산이 있다는 것을 알 수 있다. 중복되는 연산을 제거하면, 조금 더 효율적인 계산을 할 수 있다. ∂L∂θK−1=∂L∂fK∂fK∂θK−1\frac{\partial L}{\partial \theta_{K-1}} = \frac{\partial L}{\partial f_{K}}\frac{\partial f_K}{\partial \theta_{K-1}}

∂L∂θK−2=∂L∂fK∂fK∂fK−1∂fK−1∂θK−2\frac{\partial L}{\partial \theta_{K-2}} = \frac{\partial L}{\partial f_{K}}\frac{\partial f_K}{\partial f_{K-1}} \frac{\partial f_{K-1}}{\partial \theta_{K-2}} ∂L∂θK−3=∂L∂fK∂fK∂fK−1∂fK−1∂fK−2∂fK−2∂θK−3\frac{\partial L}{\partial \theta_{K-3}} = \frac{\partial L}{\partial f_{K}}\frac{\partial f_K}{\partial f_{K-1}} \frac{\partial f_{K-1}}{\partial f_{K-2}} \frac{\partial f_{K-2}}{\partial \theta_{K-3}} ∂L∂θi=∂L∂fK∂fK∂fK−1∂fK−1∂fK−2∂fK−2∂θK−3⋯∂fi+1∂θi\frac{\partial L}{\partial \theta_{i}} = \frac{\partial L}{\partial f_{K}}\frac{\partial f_K}{\partial f_{K-1}} \frac{\partial f_{K-1}}{\partial f_{K-2}} \frac{\partial f_{K-2}}{\partial \theta_{K-3}} \cdots \frac{\partial f_{i+1}}{\partial \theta_{i}}

Automatic Differentiation

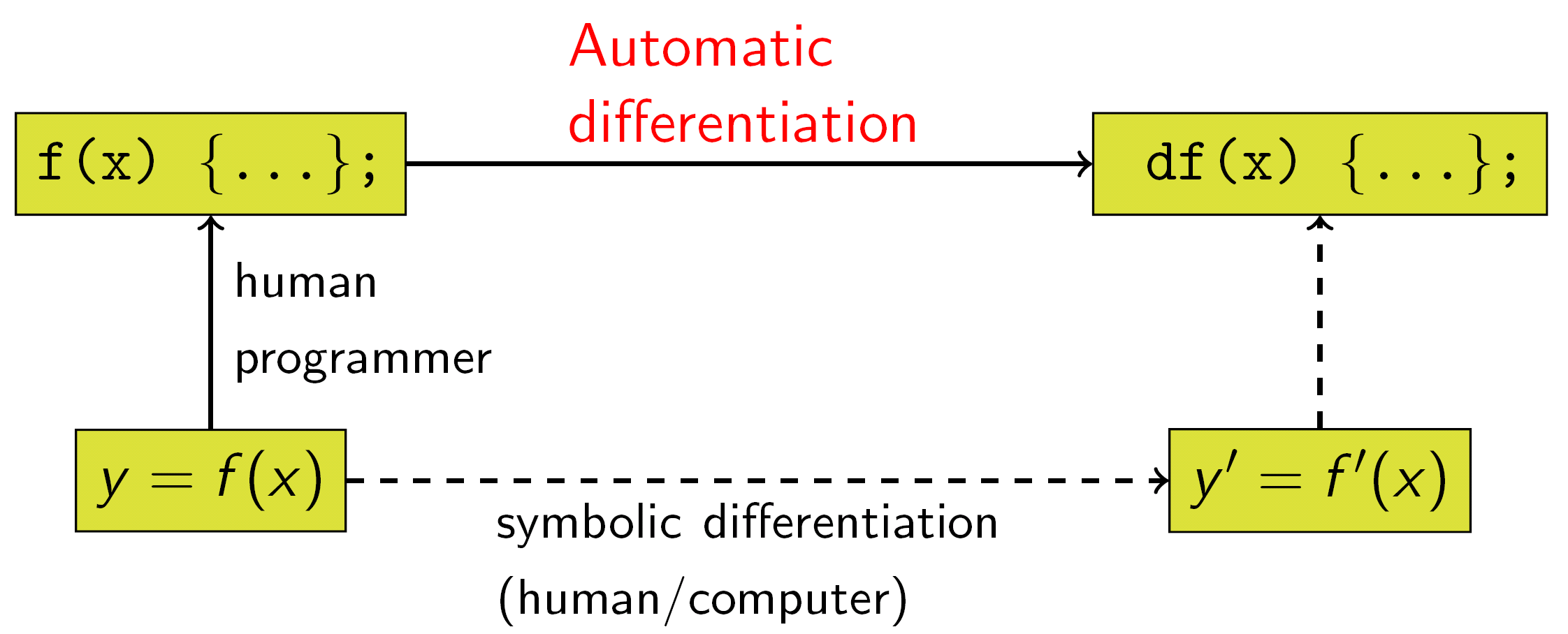
일일이 differentiation과정을 손으로 작성하거나 코드로 옮기게 되면, 실수할 일이 생길 것이다. 이런 일을 방지하고자 Automatic Differentiation이 고안되었다. 일반적으로 Addition, Muliplication, Elementry Function(e.g. Sin, Cos, Exp, Log)들은 Automatic Differentiation이 적용될 수 있다.

Automatic Differentiation에는 두 가지 모드가 있다. 이 둘의 차이는 무엇을 먼저 연산하는지이다.

다음과 같은 chain rule이 있다고 가정해보자. dydx=dydbdbdadadx\frac{dy}{dx} = \frac{dy}{db} \frac{db}{da} \frac{da}{dx}

  • Reverse Mode는 backpropagation의 순서를 따른다고 할 수 있다. 따라서, 그래프상에서는 y와 가까운 b부분 부터 연산한다. (data flow와 반대) dydx=(dydbdbda)dadx\frac{dy}{dx} = (\frac{dy}{db} \frac{db}{da} ) \frac{da}{dx}

  • Forward Mode는 reverse mode와 반대이다.(data flow와 같은 방향) dydx=dydb(dbdadadx)\frac{dy}{dx} = \frac{dy}{db} (\frac{db}{da} \frac{da}{dx})

앞으로는 Reverse Mode를 주로 다루게 되는게 가장 큰 이유는 Computation Cost가 더 낮기 때문이다.

Automatic Differentiation은 Computation Graph 형태로 나타낸다.