Linearization and Multivariate Taylor Series

gradient $\nabla f$는 함수$x_0$에서의 $f$ 를 Locally Approximation 하기 위해서 사용되기도 한다. f(x)≈f(x0)+(∇xf)(x0)(x−x0)f(x) \approx f(x_0)+(\nabla_x f)(x_0)(x - x_0)

아래의 이미지를 보면, 하나의 예시를 알 수 있다. 함수 $f$에 대해서 $x_0$에서의 근사는 아래의 이미지처럼 직선의 형태로 나타낼 수 있다.

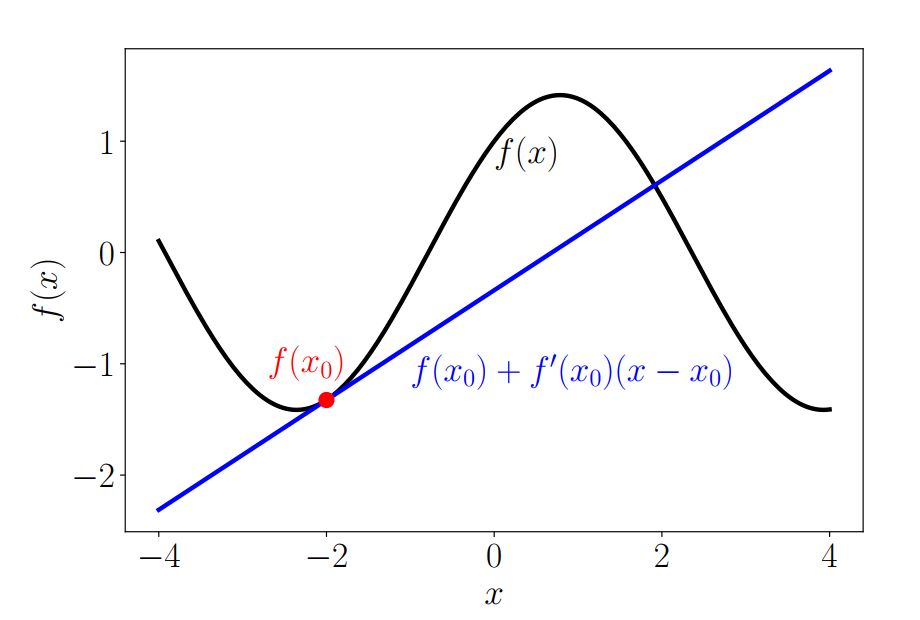
위의 근사는 $x_0$지점에서 정확할 수 있으나, 조금만 벗어나도 격차가 나기 시작합니다. 앞으로 다룰 내용은 조금 더 일반적인 근사에 대해서 다루겠다.

Definition 5.7: Multivariate Taylor Series

아래와 같은 함수 $f$가 있다고 가정하겠다. 그리고 $f$는 $x_0$에서 Smooth하다.(미분 가능하다) f:RD→Rx↦f(x),x∈RDf: R^D \rightarrow R \\ x \mapsto f(x) , x \in R^D

그리고 Difference Vector를 아래와 같이 정의해보겠다. δ=x−x0\delta = x - x_0

이제 Multivariate Taylor Series는 아래와 같이 정의할 수 있다.

  • $D^k_x f(x_0)$: k-th total derivative of f with respect to $x$, evaluated $x_0$
f(x)=∑k=0∞Dxkf(x0)k!δkf(x) = \sum_{k=0}^{\infty} \frac{D^k_x f(x_0)}{k!} \delta^k

Definition 5.8: Taylor Polynomial

  • $D^k_x f(x_0)$: k-th total derivative of f with respect to $x$, evaluated $x_0$
Tn(x)=∑k=0nDxkf(x0)k!δkT_n(x) = \sum_{k=0}^{n} \frac{D^k_x f(x_0)}{k!} \delta^k

$D^k_x$와 $\delta^k$는 모두 Higher Order Tensor이다.

아래의 $\delta^k$는 다음과 같은 차원수를 가진다. δk∈RDk\delta^k \in R^{D^k}

하나씩 살펴보겠다. 우선 $\delta^2$를 알아보겠다. δ2=δ⊗δ,δ2[i,j]=δ[i]δ[j]\delta^2 = \delta \otimes \delta, \delta^2[i, j] = \delta[i] \delta[j]

$\delta^3$을 구해보면 다음과 같다. δ3=δ⊗δ⊗δ,δ3[i,j,k]=δ[i]δ[j]δ[k]\delta^3 = \delta \otimes \delta \otimes \delta, \delta^3[i, j, k] = \delta[i] \delta[j] \delta[k]

아래의 이미지는 그 과정을 시각화한 것이다.

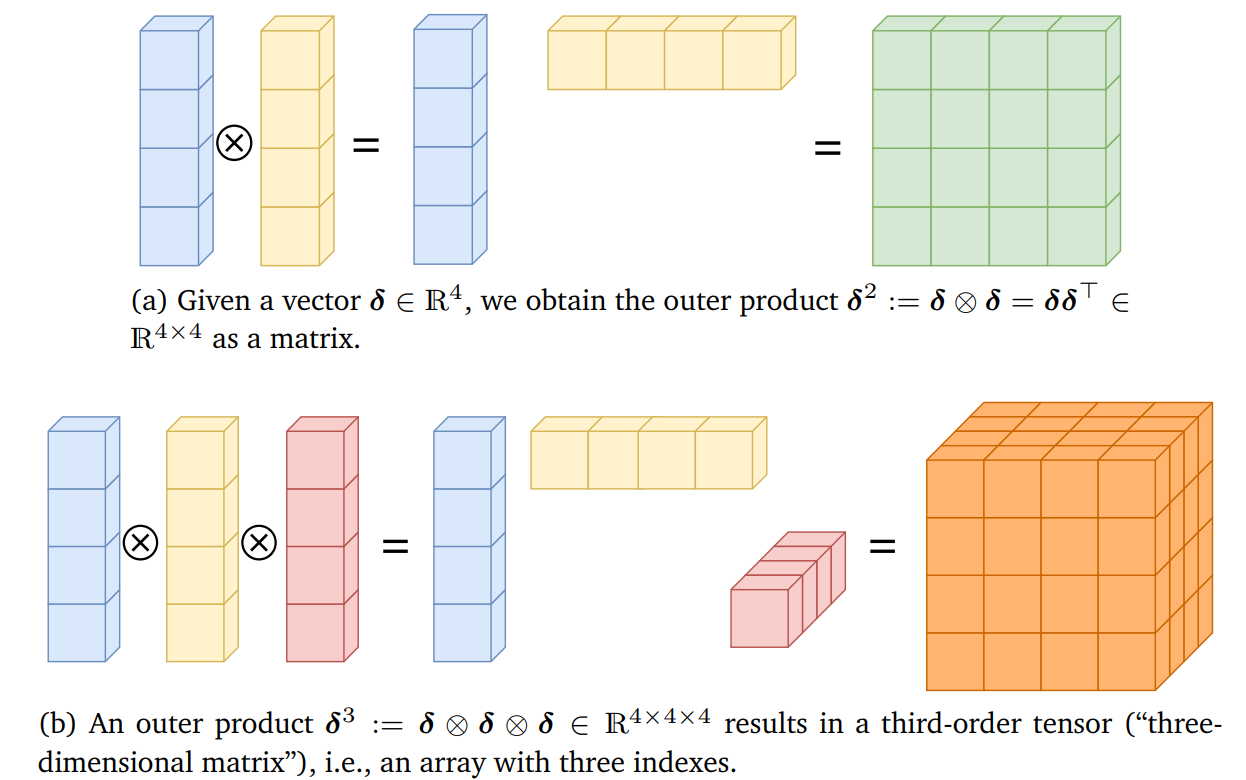
이제 아래의 수식을 살펴보자. Dx0f(x0)δk=∑i1=1D⋯∑ik=1DDxkf(x0)[i1,⋯ ,ik]δ[i1]⋯δ[ik]D^0_x f(x_0) \delta^k = \sum_{i_1=1}^D \cdots \sum_{i_k=1}^D D_x^k f(x_0)[i_1, \cdots, i_k] \delta[i_1] \cdots \delta[i_k]

  • $H(x_0)$: Hessian of f, evaluated at $x_0$

만약 $k=0$이라면, Dxkf(x0)δ0=f(x0)∈RD^k_x f(x_0) \delta^0 = f(x_0) \in R

만약 $k=1$이라면, Dx1f(x0)δ1=∇xf(x0)[i]δ[i]D^1_x f(x_0) \delta^1 = \nabla_x f(x_0)[i] \delta[i]

만약 $k=2$라면, Dx2f(x0)δ2=δTH(x0)δD^2_x f(x_0) \delta^2 = \delta^T H(x_0) \delta

만약 $k=3$라면,