Construction of a Probability Space
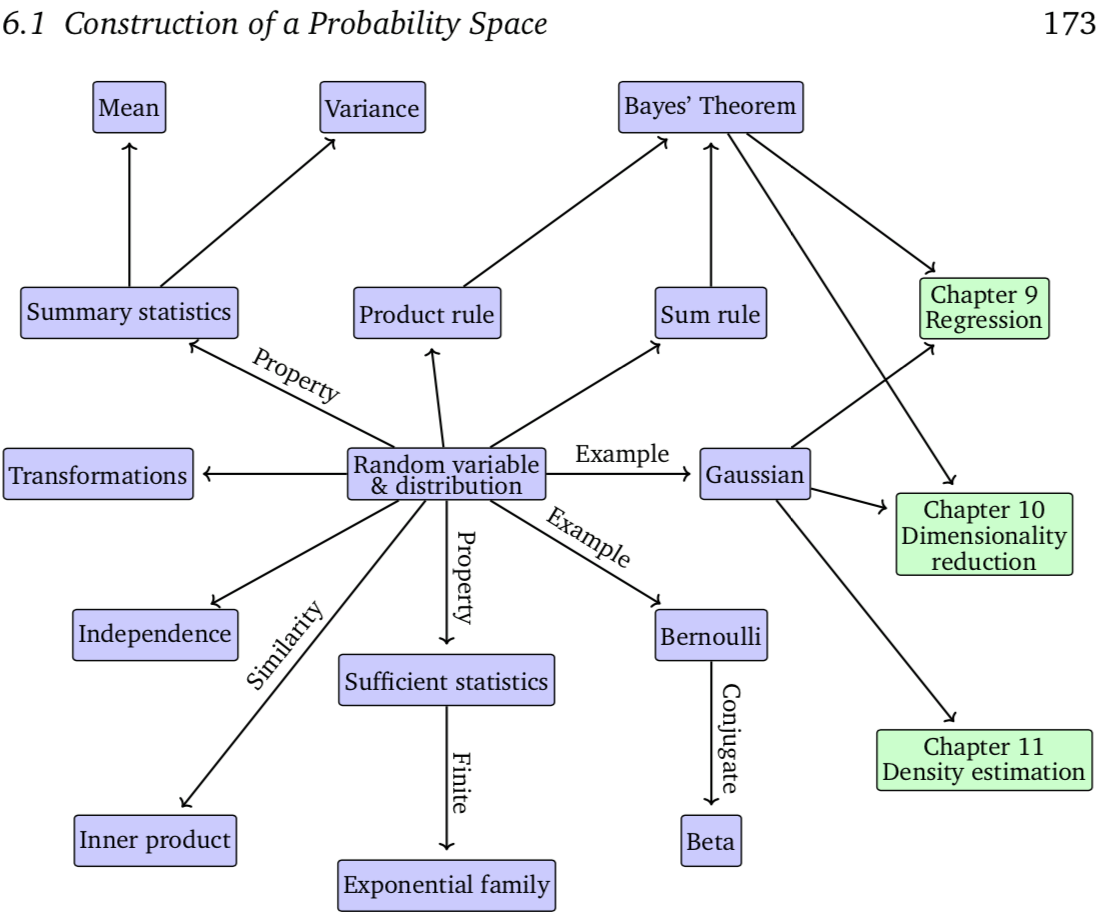
Construction of a Probability Space
확률은 간단히 말하면, 불확실성에 대한 것이다. 확률론은 실험들의 random한 결과를 수학적으로 구조화할려고 하는 것이다. 예를 들어서, 동전 던지기를 한다고 했을 때, 앞면이 나올지 뒷면이 나올지 알 수 없다. 하지만, 여러번의 시도를 하다보면, 평균적으로 앞면이 얼마나 나오는지 알 수 있다.
probability는 boolean logic의 일반화라고 볼 수 있다. boolean logic은 명확하게 결과가 나온다. 예를 들어서, 컴퓨터에 키보드로 ‘Hello World!’를 입력하면, 항상 ‘Hello World!’라는 값이 출력된다. 반면에, 확률공간은 deterministic하지 않다. 예를 들어서, 친구를 기다린다고 했을 때 다음과 같이 세가지 상황에 대해서 생각해볼 수 있다. 아래의 세가지 경우 중 어떤 일이 일어날지는 알 수 없다. 이것이 boolean logic과의 큰 차이점이다.
- 제 시간에 도착
- 교통체증으로 인한 지각
- 외계인에게 납치
probability는 machine learning부분에서 두 가지 관점에서 활용된다.
- Bayesian
- Frequentist
Probability and Random Variable
probability와 관련해서 세 가지 개념이 있다.
- probability space: probability를 측정할 수 있게 해준다.(일반적으로 random variable을 활용한다.)
- random variable: probability를 계산하기 용이한 공간으로 옮겨서 계산하게 해준다.
- distribution or law of random variable:
Probability Space
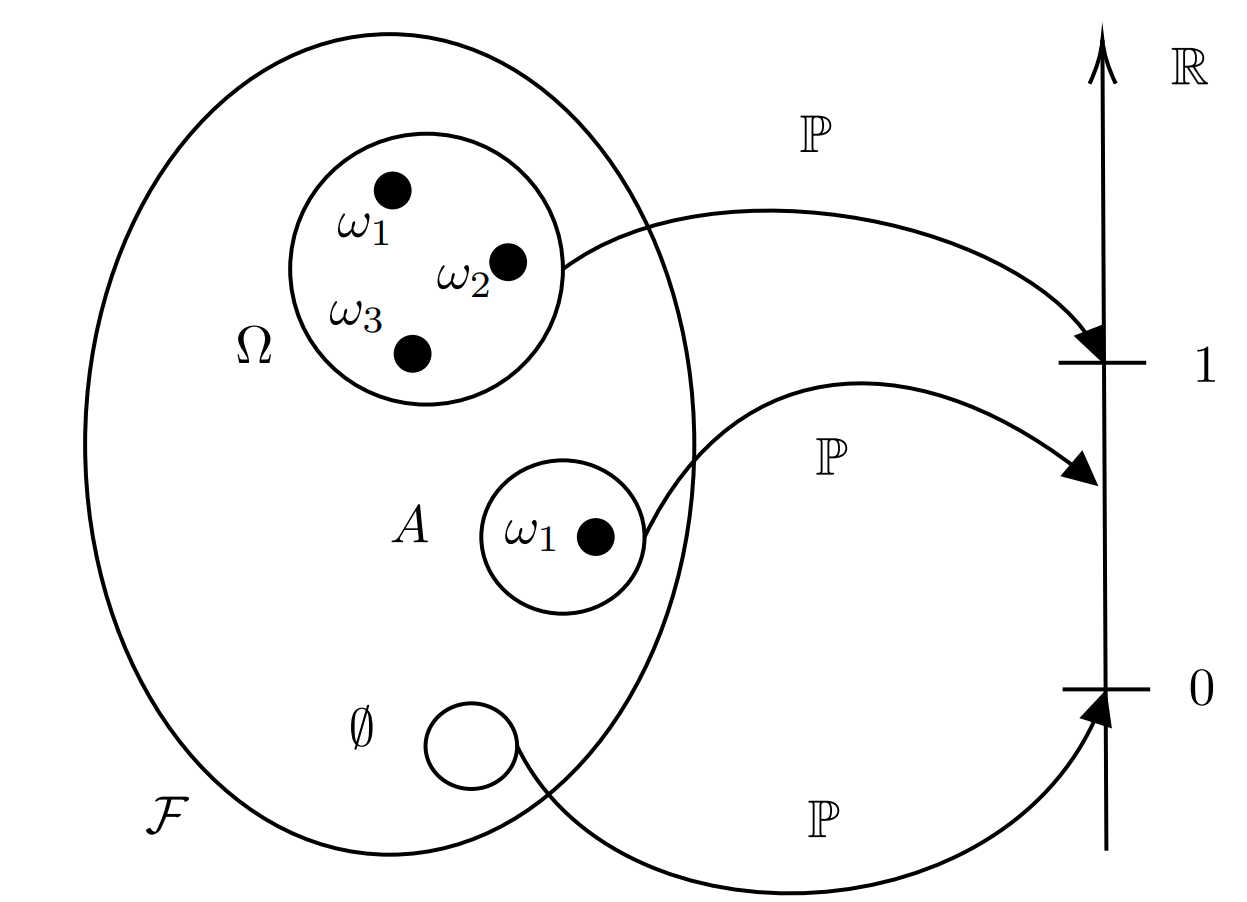
Sample Space $\Omega$
실험으로 나올 수 있는 모든 결과의 집합. 동전 두번 던지기 실험을 예로 들면 Sample Space는 아래와 같이 정해진다.
Event Space $\mathcal{A}$
실험의 잠재적인 결과의 집합. Sample Space의 부분 집합. 실험이 끝난 후에, 특정 결과가 Event Space에 포함되는지 판단할 수 있다. 종종 Event Space와 Sample Space를 혼용해서 사용하기도 한다.
Probability
Event $A \in \mathcal{A}$가 있을 때, $P(A)$를 측정할 수 있다.
어떤 Event의 Probability는 $[0, 1]$의 범위를 가지고 있고, Sample Space상의 모든 Event의 Probability의 합은 1이다.
Probability Space $\Omega, \mathcal{A}, A$가 주어졌을 때, Real-World의 현상을 Model하고 싶다.
아래와 같은 Sample Space가 있다고 가정해보겠다.
그리고, 아래와 같은 Function(Random Variable)이 있다고 가정하겠다.
- $\Tau$: target space
Target Space는 아래와 같이 정의할 수 있다. 앞으로 주목할 것은 $\Tau$의 Element의 Probability이다.
확률은 아래와 같이 정리할 수 있다.
- $S \in \Tau$
Statistics
Probability와 Statistics는 종종 혼용되는 용어이나, 이 둘은 uncertainry의 서로 다른 측면에 초점이 있다.
Probability는 Process를 Modeling하며, Random Variable을 활용하여 Uncertainty를 측정한다. 반면에, Statistics는 관측한 현상을 바탕으로 잠재적인 Process를 파악하고자 한다. 이런점에서 Machine Learning은 Statistics에 가까운데, ML에서는 주어진 데이터를 재현할 수 있는 모델을 만드는 것이 목표이기 때문이다.
Machine Learning에서 중요한 이슈 중 하나는 Generalization Error이다. 이는 현재 실험에서뿐만 아니라, 미래에 다른 실험에서도 좋은 성능을 내는 것을 기대한다는 것이다.
Discrete and Continuous Probabilities
Target Space의 성질에 따라서 Distribution의 종류도 달라진다. 앞으로의 내용은 Discrete Probability와 Continous Probability를 다룰 계획이다.
Discrete Probability
Target Space가 Discrete한 경우이다. 아래 이미지와 같이 Multiple Random Variable이 있다고 해보자.
- $X, Y$: Random Variables
- Target Space: 각 Random Variable($X, Y$) 의 Target Space의 곱집합
이를 바탕으로 Joint Probability를 정의할 수 있다.
- $n_{ij}$: $x_i$, $y_j$ 가 발생한 횟수
- $N$: 전체 횟수
Joint Probability를 정의하고 나면, 사실 위의 이미지가 PMF(Probability Mass Function) 이라는 것을 알 수 있다. 그리고 Probability라는 것이 결국은 State(Event)를 입력으로 받고 Real을 출력으로 가지는 함수라는 것을 알 수 있다.
Marginal Probability $p(x)$는 Joint Distribution $p(x, y)$에서 $X$가 입력으로 $Y$와 무관하게 $x$를 받는 것이다.
Conditional Probability $p (y \given x)$ 는 $X =x$ 인 경우에서 $Y=y$일 때의 Probability이다.
Continous Probability
이번 섹션에서는 Real-Valued Random Variable를 다룰 것이다. Target Space는 실수공간에서의 Interval이라고 볼 수 있다.
Definition: Probability Density Function
함수 $f: \R^D \rightarrow R$ 는 아래의 조건을 만족하면, Probability Density Function이라고 정의한다.
-
$\forall x \in R^D: f(x) \geqslant 0$
-
Integral이 존재하며, 다음과 같은 조건을 만족
Probability Density Function은 Probability Mass Function과 달리, point $X=x$에서의 Probability가 0이다. PDF에서는 Probability를 Interval로 측정한다.
Definition: Cumulative Distribution Function
- $X = [X_1, \cdots , X_D]^T$
- $x = [x_1, \cdots , x_D]^T$
Contrasting Discrete and Continous Distribution
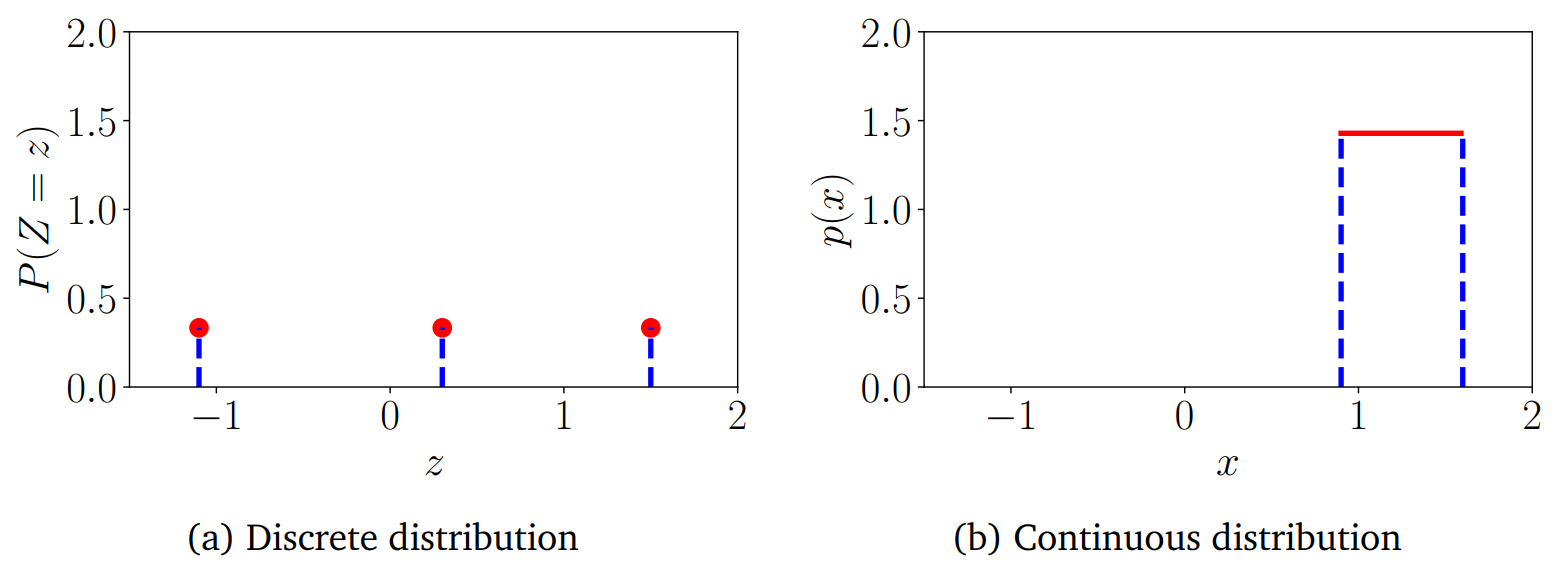
Discrete Random Variable일 경우, Mass가 $[0, 1]$사이의 값을 가지지만, Continous Random Variable같은 경우에는 Density가 $[0, 1]$사이의 값을 가지지 않는다. 위의 이미지는 Discrete/Continous Uniform Distribution을 나타낸 것이다.