우리는 Random Variable을 요약하고 싶어하며, 요약된 결과는 Deterministic하다. 이런 정보는 Random Variable의 특성을 파악하는데 도움을 준다. 이번 장에서는 Mean과 Variance에 대해서 다룰 것이다. 그리고 Random Variable을 비교하는 방법에 대해서 다룰 것이다.
두 Random Variable의 독립성
두 Random Variabler간의 Inner Product
$\mathcal{X}$: Random Variable의 Target Space, Possible Outcome
Univariate Continuous Random Variable $X ~ p(x)$아래에서 함수 g $g: R \rightarrow R$의 Expected value는 아래와 같이 정의된다.
E x [ g ( x ) ] = ∫ X g ( x ) p ( x ) d x \mathbb{E}_x[g(x)] = \int_{\mathcal{X}}g(x) p(x) dx E x [ g ( x ) ] = ∫ X g ( x ) p ( x ) d x Discrete Random Variable일 경우에는 아래와 같이 구할 수 있다.
E x [ g ( x ) ] = ∑ x ∈ X g ( x ) p ( x ) \mathbb{E}_x[g(x)] = \sum_{x\in \mathcal{X}} g(x)p(x) E x [ g ( x ) ] = x ∈ X ∑ g ( x ) p ( x ) Remark: Multivariate Case
E x [ g ( x ) ] = [ E X 1 [ g ( x 1 ) ] E X 2 [ g ( x 2 ) ] ⋮ E X n [ g ( x n ) ] ⋮ ] ∈ R n \mathbb{E}_x[g(x)] = \begin{bmatrix} \mathbb{E}_{X_1}[g(x_1)] \\ \mathbb{E}_{X_2}[g(x_2)] \\ \vdots \\ \mathbb{E}_{X_n}[g(x_n)]\vdots \end{bmatrix} \in R^{n} E x [ g ( x ) ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ E X 1 [ g ( x 1 ) ] E X 2 [ g ( x 2 ) ] ⋮ E X n [ g ( x n ) ] ⋮ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∈ R n Example
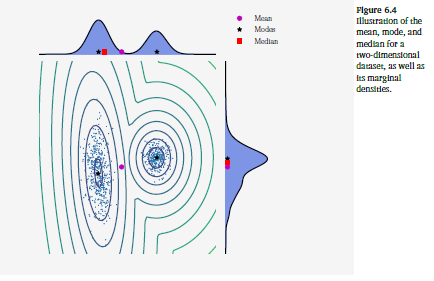
위 이미지의 분포를 수식으로 나타내면 아래와 같다.
p ( x ) = 0.4 ⋅ N ( x ∣ [ 10 2 ] , [ 1 0 0 1 ] ) + 0.6 ⋅ N ( x ∣ [ 0 0 ] , [ 8.4 2.0 2.0 1.7 ] ) p(x) = 0.4 \cdot \mathcal{N}(x \mid \begin{bmatrix} 10 \\ 2\end{bmatrix}, \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}) + 0.6 \cdot \mathcal{N}(x \mid \begin{bmatrix} 0 \\ 0\end{bmatrix}, \begin{bmatrix} 8.4 & 2.0 \\ 2.0 & 1.7 \end{bmatrix}) p ( x ) = 0 . 4 ⋅ N ( x ∣ [ 1 0 2 ] , [ 1 0 0 1 ] ) + 0 . 6 ⋅ N ( x ∣ [ 0 0 ] , [ 8 . 4 2 . 0 2 . 0 1 . 7 ] ) 위의 분포의 Expected Value는 다음과 같이 구할 수 있다.
E X [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ [ a g ( x ) + b h ( x ) ] p ( x ) d x = a ∫ g ( x ) p ( x ) d x + b ∫ h ( x ) p ( x ) d x = a E X [ g ( x ) ] + b E X [ h ( x ) ] \mathbb{E}_X[f(x)] = \int{f(x) p(x) dx} = \int {[ag(x) + bh(x)] p(x) dx} \\ = a \int{g(x)p(x) dx} + b \int{h(x)p(x)dx} = a \mathbb{E}_X[g(x)] + b \mathbb{E}_X[h(x)] E X [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ [ a g ( x ) + b h ( x ) ] p ( x ) d x = a ∫ g ( x ) p ( x ) d x + b ∫ h ( x ) p ( x ) d x = a E X [ g ( x ) ] + b E X [ h ( x ) ]
$X$ state $x \in R^D$Random Variable의 Mean은 아래와 같이 정의된다.
E x [ x ] = [ E X 1 [ x 1 ] E X 2 [ x 2 ] ⋮ E X n [ x n ] ⋮ ] ∈ R n \mathbb{E}_x[x] = \begin{bmatrix} \mathbb{E}_{X_1}[x_1] \\ \mathbb{E}_{X_2}[x_2] \\ \vdots \\ \mathbb{E}_{X_n}[x_n]\vdots \end{bmatrix} \in R^{n} E x [ x ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ E X 1 [ x 1 ] E X 2 [ x 2 ] ⋮ E X n [ x n ] ⋮ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∈ R n Continuous Random Variable
E x d [ x d ] = ∫ X x d p ( x d ) d x d \mathbb{E}_{x_d}[x_d] = \int_{\mathcal{X}}x_dp(x_d) dx_d E x d [ x d ] = ∫ X x d p ( x d ) d x d Discrete Random Variable
E x [ x ] = ∑ x d ∈ X X x i p ( x d = x i ) \mathbb{E}_x[x] = \sum_{x_d\in \mathcal{X}}^{\mathcal{X}} x_ip(x_d=x_i) E x [ x ] = x d ∈ X ∑ X x i p ( x d = x i )
두 Random Variable $X, Y \in R$의 Covariance는 아래와 같이 정의된다.
C o v X , Y [ x , y ] = E X , Y [ ( x − E X [ x ] ) ( y − E Y [ y ] ) ] \mathbf{Cov}_{X, Y}[x, y] = \mathbb{E}_{X,Y}[(x - \mathbf{E}_X[x])(y - \mathbf{E}_Y[y])] C o v X , Y [ x , y ] = E X , Y [ ( x − E X [ x ] ) ( y − E Y [ y ] ) ] 위의 수식은 아래와 같이 전개할 수 있다.
C o v X , Y [ x , y ] = E [ x y ] − E ( x ) E ( y ) \mathbf{Cov}_{X, Y}[x, y] = \mathbb{E}[xy] - \mathbb{E}(x) \mathbb{E}(y) C o v X , Y [ x , y ] = E [ x y ] − E ( x ) E ( y )
$\mathbf{Cov}[x, x] = \mathbf{Var}(x)$
$\sqrt{\mathbf{Var}(x)} = \sigma{x}$
두 Multivariate Random Variable $X \in R^D, Y \in R^E$는 아래와 같이 정의된다.
C o v [ x , y ] = E [ x y T ] − E ( x ) E ( y ) = C o v [ y , x ] T ∈ R D × E \mathbf{Cov}[x, y] = \mathbb{E}[xy^T] - \mathbb{E}(x) \mathbb{E}(y) = \mathbf{Cov}[y, x] ^T \in R^{D \times E} C o v [ x , y ] = E [ x y T ] − E ( x ) E ( y ) = C o v [ y , x ] T ∈ R D × E 직관적으로는 Random Variable의 퍼짐정도를 나타낸다. Multivariate Random Variable의 경우에는 각 Element가 Random Variable의 Dimemsion간의 관계를 의미한다.
Random Variable $X$ with states $x \in R^D$의 Variance는 아래와 같이 정의된다.
V X ( x ) = C o v X [ x , x ] = E X [ ( x − u ) ( x − u ) T ] = E X [ x x T ] − E [ x ] E [ x ] T = [ C o v [ x 1 , x 1 ] C o v [ x 1 , x 2 ] ⋯ C o v [ x 1 , x D ] ⋮ ⋮ ⋱ ⋮ C o v [ x D , x 1 ] C o v [ x D , x 2 ] ⋯ C o v [ x D , x D ] ] \mathbb{V}_X(x) = \mathbf{Cov}_X[x,x] = \mathbf{E}_X[(x-u)(x-u)^T] = \mathbf{E}_X[xx^T] - \mathbb{E}[x]\mathbf{E}[x]^T \\ = \begin{bmatrix} \mathbf{Cov}[x_1, x_1] & \mathbf{Cov}[x_1, x_2] & \cdots & \mathbf{Cov}[x_1, x_D] \\ \vdots & \vdots & \ddots & \vdots \\
\mathbf{Cov}[x_D, x_1] & \mathbf{Cov}[x_D, x_2] & \cdots & \mathbf{Cov}[x_D, x_D]
\end{bmatrix} V X ( x ) = C o v X [ x , x ] = E X [ ( x − u ) ( x − u ) T ] = E X [ x x T ] − E [ x ] E [ x ] T = ⎣ ⎢ ⎢ ⎡ C o v [ x 1 , x 1 ] ⋮ C o v [ x D , x 1 ] C o v [ x 1 , x 2 ] ⋮ C o v [ x D , x 2 ] ⋯ ⋱ ⋯ C o v [ x 1 , x D ] ⋮ C o v [ x D , x D ] ⎦ ⎥ ⎥ ⎤
두 Random Variable의 Correlation은 아래와 같이 정의된다.
c o r r [ x , y ] = C o v [ x , y ] V [ x ] V [ y ] ∈ [ − 1 , 1 ] \mathbf{corr}[x, y] = \frac{\mathbf{Cov}[x, y]}{ \sqrt{\mathbb{V}[x]\mathbb{V}[y]} }\in [-1, 1] c o r r [ x , y ] = V [ x ] V [ y ] C o v [ x , y ] ∈ [ − 1 , 1 ]
위에서 살펴본 통계값은 Population Mean/Covariance이다.
일반적으로 Machine Learning에서는 관측값을 바탕으로 통계값을 추정한다.
Random Variable X를 고려해보자.
Population Statistics에서 Empirical Statistics로 가는 두 가지 방법이 있다.
한정된 데이터셋을 Empirical Statistics를 구하기 위해 사용한다. Empirical Statistics을 한정된 Random Variable에 대한 함수로 생각한다.
데이터를 관측한다. 이를 Random Variable의 결과로 본다. Empirical Statistics를 적용한다.
x ˉ : = 1 N ∑ n = 1 N x n , \bar{x} := \frac{1}{N} \sum_{n=1}^N x_n, x ˉ : = N 1 n = 1 ∑ N x n , Σ : = 1 N ∑ n = 1 N ( x n − x ˉ ) ( x n − x ˉ ) \Sigma := \frac{1}{N} \sum_{n=1}^N (x_n - \bar{x})(x_n - \bar{x}) Σ : = N 1 n = 1 ∑ N ( x n − x ˉ ) ( x n − x ˉ )
Covariance는 Squared Deviation의 Expectation으로 구할 수 있다.
V X [ x ] : = E X [ ( x − u ) 2 ] \mathbf{V}_X[x] := \mathbf{E}_X[(x-u)^2] V X [ x ] : = E X [ ( x − u ) 2 ] 위의 식을 통해서 Covariance를 구할려면 아래와 같이 두 가지 과정을 거쳐야한다.
$u$를 구한다.
$u$를 통해서 Variance를 구한다.
하지만 아래 수식을 통하면 이런 과정을 거치지 않아도 된다. 한번의 과정을 통해서 구할 수 있다.
V X [ x ] : = E X [ x 2 ] − ( E X [ x 2 ] ) 2 \mathbf{V}_X[x] := \mathbf{E}_X[x^2] - (\mathbf{E}_X[x^2])^2 V X [ x ] : = E X [ x 2 ] − ( E X [ x 2 ] ) 2 하지만 위의 수식은 Numerically Unstable하다는 한계를 가지고 있다.
Variance를 표현하는 다른 방법은 데이터들의 모든 쌍에 대해서 차이의 평균을 구하는 것이다.
1 N 2 ∑ i , j = 1 N ( x i − x j ) 2 = 2 [ 1 N ∑ i = 1 N x i 2 − ( 1 N ∑ i = 1 N x i ) 2 ] \frac{1}{N^2} \sum_{i,j=1}^N(x_i - x_j)^2 = 2[\frac{1}{N}\sum_{i=1}^Nx_i^2 - (\frac{1}{N}\sum_{i=1}^Nx_i)^2] N 2 1 i , j = 1 ∑ N ( x i − x j ) 2 = 2 [ N 1 i = 1 ∑ N x i 2 − ( N 1 i = 1 ∑ N x i ) 2 ] Random Variable $x, y \in R^D$
E [ x + y ] = E [ x ] + E [ y ] \mathbf{E}[x+y] = \mathbf{E}[x] + \mathbf{E}[y] E [ x + y ] = E [ x ] + E [ y ] E [ x − y ] = E [ x ] − E [ y ] \mathbf{E}[x-y] = \mathbf{E}[x] - \mathbf{E}[y] E [ x − y ] = E [ x ] − E [ y ] V [ x + y ] = V [ x ] + V [ y ] + C o v [ x , y ] + C o v [ y , x ] \mathbf{V}[x+y] = \mathbf{V}[x] + \mathbf{V}[y] + \mathbf{Cov}[x, y] + \mathbf{Cov}[y, x] V [ x + y ] = V [ x ] + V [ y ] + C o v [ x , y ] + C o v [ y , x ] V [ x + y ] = V [ x ] + V [ y ] − C o v [ x , y ] − C o v [ y , x ] \mathbf{V}[x+y] = \mathbf{V}[x] + \mathbf{V}[y] - \mathbf{Cov}[x, y] - \mathbf{Cov}[y, x] V [ x + y ] = V [ x ] + V [ y ] − C o v [ x , y ] − C o v [ y , x ] $y = Ax + b$라는 Random Variable의 Statistic는 $X$로 아래와 같이 표현될 수 있다.
E Y [ y ] = E X [ A x + b ] = A E X [ x ] + b = A u + b \mathbf{E}_Y[y] = \mathbf{E}_X[Ax + b] = A \mathbf{E}_X[x] + b = Au + b E Y [ y ] = E X [ A x + b ] = A E X [ x ] + b = A u + b V Y [ y ] = V X [ A x + b ] = A V X [ x ] A T = A Σ A T \mathbf{V}_Y[y] = \mathbf{V}_X[Ax + b] = A \mathbf{V}_X[x]A^T = A\Sigma A^T V Y [ y ] = V X [ A x + b ] = A V X [ x ] A T = A Σ A T C o v [ x , y ] = E [ x ( A x + b ) T ] − E [ x ] E [ A x + b ] T = E [ x ] b T + E [ x x T ] A T − u b T − u u T A T = u b T − u b T + ( E [ x x T ] − u u T ) A T = Σ A T \mathbf{Cov}[x,y]= \mathbf{E}[x(Ax + b)^T] - \mathbf{E}[x]\mathbf{E}[Ax + b]^T \\
= \mathbf{E}[x]b^T + \mathbf{E}[xx^T]A^T - u b^T - uu^TA^T \\
= ub^T - ub^T + (\mathbf{E}[xx^T] - uu^T)A^T
= \Sigma A^T C o v [ x , y ] = E [ x ( A x + b ) T ] − E [ x ] E [ A x + b ] T = E [ x ] b T + E [ x x T ] A T − u b T − u u T A T = u b T − u b T + ( E [ x x T ] − u u T ) A T = Σ A T
p ( x , y ) = p ( x ) p ( y ) p(x, y) = p(x) p(y) p ( x , y ) = p ( x ) p ( y ) Random Variable X, Y가 독립이라는 것은 y에 대한 정보를 알아도 x에 추가적인 정보가 없는 것을 의미한다.
그리고 아래와 같은 관계가 성립한다.
$p(x \mid y) = p(x)$
$p(y \mid x) = p(y)$
$\mathbf{V}{X, Y}[x+ y] = \mathbf{V} {X}[x] + \mathbf{V}_{Y}[y]$
$\mathbf{Cov}_{X,Y}[x, y ] = 0$
(Remark ) Covariance가 0이라고 독립이지는 않다. Covariance는 Linear Depedence만 측정한다. 만약 Non-Linearly Dependent하다면 Covariance는 0이지만, Statistically Dependent하다.
x y = x 2 x \\
y =x^2 x y = x 2
p ( x , y ∣ z ) = p ( x ∣ z ) p ( y ∣ z ) for all z ∈ Z p(x, y \mid z) = p(x \mid z) p(y \mid z) \ \text{ for all }\ z\in Z p ( x , y ∣ z ) = p ( x ∣ z ) p ( y ∣ z ) for all z ∈ Z 직관적으로 Random Variable X, Y는 z라는 정보가 주어지면 독립이라는 의미이다.
Product Rule을 통해서 아래와 같이 전개 가능하다.
p ( x , y ∣ z ) = p ( x ∣ y , z ) p ( y ∣ z ) p(x, y\mid z) = p(x \mid y, z) p(y \mid z) p ( x , y ∣ z ) = p ( x ∣ y , z ) p ( y ∣ z )
위의 식을 통해서 아래와 같은 관계를 구할 수 있다. z가 주어지면 x, y는 독립을 표현해준다.
p ( x ∣ y , z ) = p ( x ∣ z ) p(x \mid y, z)=p(x \mid z) p ( x ∣ y , z ) = p ( x ∣ z )
두 Random Variable이 Uncorrelated하다면 다음과 같은 관계가 성립한다.
V [ x + y ] = V [ x ] + V [ y ] \mathbb{V}[x+y] = \mathbb{V}[x] + \mathbb{V}[y] V [ x + y ] = V [ x ] + V [ y ] c 2 = a 2 + b 2 c^2 = a^2 + b^2 c 2 = a 2 + b 2
Random Variable은 백터공간에서 백터로 표현할 수 있다. 두 Random Variable의 Inner Product은 아래와 같이 표현한다.
이때 두 Random Variable의 Mean은 모두 0이라고 가정한다.
< X , Y > : = C o v [ x , y ] <X, Y> := \mathbf{Cov}[x, y] < X , Y > : = C o v [ x , y ]
Symmetric
Positive Definite
Linear in Either Arguments
Random Variable X의 Norm은 다음과 같이 구할 수 있다.
∥ X ∥ = C o v [ x , x ] = V [ x ] = σ ( x ) \rVert X \rVert = \sqrt{\mathbf{Cov}[x,x]} = \sqrt{\mathbb{V}[x]} = \sigma(x) ∥ X ∥ = C o v [ x , x ] = V [ x ] = σ ( x )
이제 두 Random Variable의 각도를 구해보자. Correlation은 두 Random Variable의 코사인 각도로 볼 수 있다.
cos θ = < X , Y > ∥ X ∥ ∥ Y ∥ = C o v [ x , y ] V [ x ] V [ y ] \cos \theta = \frac{<X, Y>}{\rVert X \rVert \rVert Y \rVert} = \frac{\mathbf{Cov}[x, y]}{\sqrt{\mathbb{V}[x] \mathbb{V}[y]}} cos θ = ∥ X ∥ ∥ Y ∥ < X , Y > = V [ x ] V [ y ] C o v [ x , y ]
선형대수학에서 Inner Product의 결과가 0일경우 서로 독립이라고 한다. 이와 대응되는 것으로 Random Variable간의 독립은 $\mathbf{Cov}[x, y] = 0$일 때 서로 Uncorrelated하다고 한다.