Continuous Optimization

  • Unconstrained Optimization
  • Constrained Optimization

Optimization Using Gradient Descent

  • $f: R^D \rightarrow R$
  • $f$는 미분가능
min⁡xf(x)\min_x f(x)

Gradient Descent는 First Order Optimization 방법이다. Minimum을 찾기 위해서는 함수의 Gradient의 반대방향(Negative)로 적절하게 이동해야한다.

  • $\gamma > 0$: Small Step Size
  • $f: R^n \rightarrow R$
x1=x0−γ(∇f(x0))Tx_1 = x_0 - \gamma (\nabla f (x_0))^T

Step Size

Gradient Descent에서는 적절한 크기의 Step Size를 고르는 것이 중요하다. Step Size가 너무 작다면 수렴하는 속도가 느려지고 너무 크다면 수렴자체가 힘들 수 있다. 모멘텀을 사용하게 되면 Optimization 문제가 Smooth해지는 효과를 기대할 수 있는데 이는 추후에 다루겠다.

적절한 Step Size를 고르는 Heuristics가 있다.

  • Gradient Step후 함수값이 증가한다면 이를 진행하기 전으로 되돌리고 Step Size를 감소시킨다.
  • Gradient Step후 함수값이 감소한다면 Step Size를 더 늘려본다.

Gradient Descent with Momentum

만약 Optimization Surface의 Curvature이 제대로 Scale되지 않은 부분이 있다면 Gradient Descent의 수렴속도는 매우 느릴 수 있다. Curvature는 Gradient Descent Step이 만날 수 있는 벽 혹은 협곡이며 이때 Gradient Descent의 방향을 기억하고 있으면 해결하는데 도움이 된다.

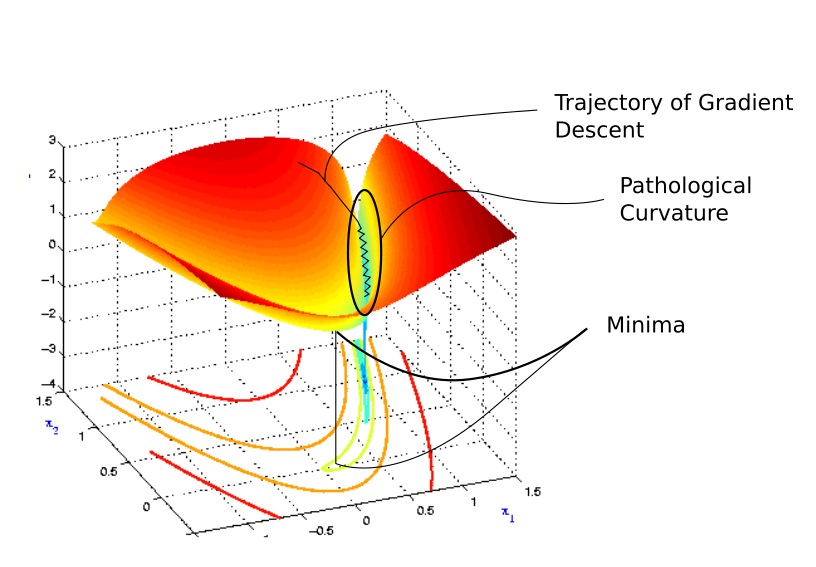
Momentum이란 이전 Iteration의 Gradient 방향을 일부 반영하는 것을 의미한다.

  • $\alpha \in [0, 1]$
xi+1=xi−γi(∇f(xi))T+αΔxix_{i+1} = x_i - \gamma_i (\nabla f (x_i))^T + \alpha \Delta x_i Δxi=xi−xi−1=αΔxi−1−γ(∇f(xi−1))T\Delta x_i = x_i - x_{i-1} = \alpha \Delta x_{i-1} - \gamma (\nabla f (x_{i-1}))^T

Stochastic Gradient Descent

Gradient를 계산하는 과정은 상당히 비싸다. 따라서 조금 더 낮은 연산비용으로 비슷한 효과를 가질 수 있는 Stochastic Gradient Descent에 대해서 다루겠다.

여기서 Stochastic이라는 말은 데이터셋에서 샘플링하여 Gradient를 계산하겠다는 뜻이다.

  • $x_n \in R^D$: Training Inputs
  • $y_n$: Training Targets
  • $\theta$: Parameter
L(θ)=∑n=1NLn(θ)=−∑n=1Nlog⁡p(yn∣xn,θ)L(\theta) = \sum_{n=1}^N L_{n}(\theta) = -\sum_{n=1}^N \log p(y_n \mid x_n, \theta) θi+1=θi−γi(∇L(θi))T=θi−γi∑n=1N(∇Ln(θi))T\theta_{i+1} = \theta_{i} -\gamma_i(\nabla L(\theta_i))^T = \theta_i - \gamma_i \sum_{n=1}^N (\nabla L_n (\theta_i))^T

만약 Training set이 너무 크다면, Training set중 일부만 사용해서 Gradient를 구할 수 있으며 이를 Stochastic Gradient Descent라고 한다. 전체 Training set을 사용하는 것보다 빠르고 가볍게 계산할 수 있다는 장점이 있다. 하지만 Gradient의 Variance는 커지게 되어 정확도가 떨어진다는 단점이 있다.