Diagonal Matrix

D=[c11000c22000c33]D = \begin{bmatrix} c_{11} & 0 & 0 \\0 & c_{22} & 0 \\ 0 & 0 & c_{33}\end{bmatrix}

$c_{ii}$외의 나머지 성분이 모두 0인 행렬을 diagonal matrix라고 부른다. diagonal matrix는 낮은 computation으로 아래와 같은 것들을 구할 수 있다.

  • determinant같은 경우는 대각성분의 곱으로 구할 수 있다.
  • $D^N$같은 경우에는 각 성분에 N제곱을 한 matrix이다.
  • $D^{-1}$은 대각성분에 역수를 취하면 된다. (대각성분은 모두 0이 아니여야한다.)

이번 시간에는 matrix를 diagnoal matrix형태로 표현하는 방법에 대해서 정리해볼 것이다.

Diagonalizable

matrix $A \in R^{m \times n}$ diagonal matrix와 similar한 관계를 가질 수 있으면, diagonalizable하다고 한다.

이 때, $P^{-1}$이 존재해야 한다. D=P−1APD = P^{-1}AP

Remark

A와 D가 similar하다는 것은 basis change에서 아래와 같은 조건이 성립한다는 것이다. A=P−1DPA = P^{-1}DP 위의 Diagonalization을 eigendecomposition이라고 하며, 결국 eigendecomposition은 한 matrix를 다른 basis에서 보여주는 것이다. 뒤에서 다루겠지만, 여기서 사용되는 basis는 결국 eigenvector이다.

$A \in R^{n \times n}$은 $\lambda_1, \cdots, \lambda_n$의 scalar set이 있고 $p_1, \cdots, p_n \in R^{n}$이 있다고 하자.

만약 A가 diagonalizable하다면, 아래와 같은 수식이 성립한다. 결론부터 말하면, 결국 P가 eigenvector로 이루어진 matrix이고 D가 eigenvalue로 이루어진 matrix여야 diagnalizable하다. AP=PDAP = PD

AP=A[p1,⋯ ,pn]=[Ap1,⋯ ,Ap2]PD=[p1,⋯ ,pn][λ11⋯0⋮⋱⋮0⋯λnn]=[p1λ11,⋯ ,pnλnn]AP = A [p_1, \cdots, p_n] = [Ap_1, \cdots, Ap_2] \\ PD = [p_1, \cdots, p_n] \begin{bmatrix} \lambda_{11} & \cdots & 0 \\\vdots & \ddots & \vdots \\ 0 & \cdots& \lambda_{nn}\end{bmatrix} = [p_1\lambda_{11}, \cdots, p_n\lambda_{nn}]

위의 식을 vector관점에서 보면 아래와 같다. Ap1=λ1p1Ap2=λ2p2Ap3=λ3p3⋮Apn=λnpnAp_1 = \lambda_1p_1 \\ Ap_2 = \lambda_2p_2 \\ Ap_3 = \lambda_3p_3 \\ \vdots \\ Ap_n = \lambda_np_n \\ 따라서, $p_i$는 eigenvector이고, $\lambda_i$는 eigenvalue이다.

Eigendecomposition

Theorem 4.20 (Eigendecomposition)

square matrix $A \in R^{n \times n}$은 아래와 같이 분해될 수 있다. A=PDP−1A = PDP^{-1}

  • $P \in R^{n \times n}$
  • $D$: diagonal matrix, 대각성분은 eigenvalue

Theorem 4.20에 따르면, non-defective matrix만이 diagonalizable하다.

Theorem 4.21. A symmetric matrix $S \in R^{n×n}$ can always be diagonalized.

spectral theorem과 유사하다.

Geometric Intuition for the Eigendecomposition

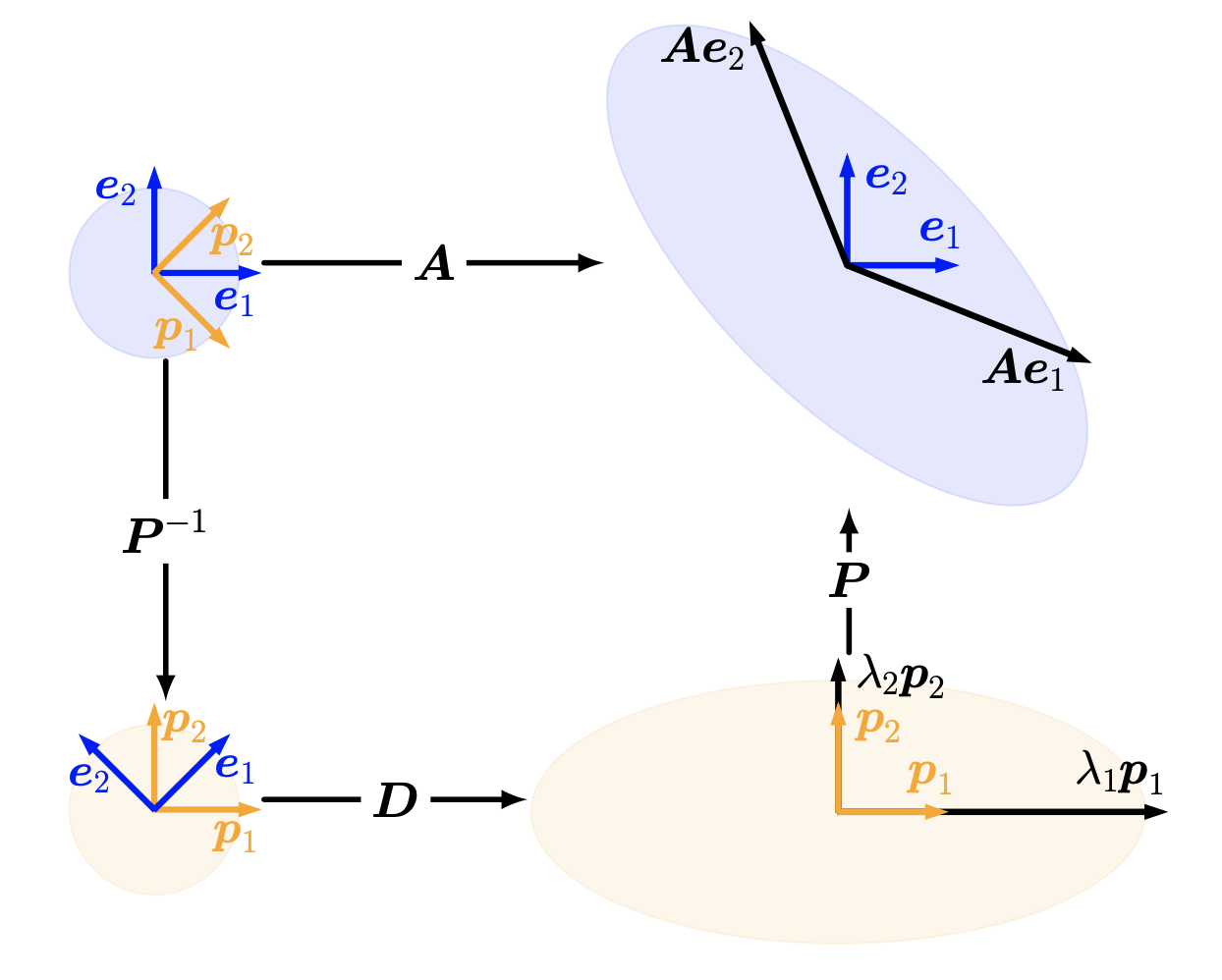
위의 이미지는 A라는 linear transformation을 eigendecomposition한 것이다.

$P$는 eigenvector로 이루어져 있다. 따라서, $P^{-1}$ linear transform을 하게되면, eigenvector가 basis인 공간으로 가게된다. 그리고 D는 각 eigenbais를 scale해주는 역할을 하며, 각 성분은 eigenvalue이다. 그리고 마지막으로 $P$를 다시 적용하면 원래의 standard bais로 돌아오게 된다.

eigendecomposition은 몇 가지 이점이 있다.

  • Power를 효율적으로 계산

  • An=(PDP−1)n=PDnP−1A^n = (PDP^{-1})^n = PD^nP^{-1}
  • determinant를 효율적으로 계산 det(A)=det(PDP−1)=det(PP−1D)=det(D)=∏i=1nλidet(A) = det(PDP^{-1})=det(PP^{-1}D) = det(D) = \prod_{i=1}^n \lambda_i