Singular Value Decomposition 정리글

• Singular Value Decomposition
  • Theorem 4.22 (SVD Theorem)
• Geometric Intuitions for the SVD
  • Construction of the SVD
    • 1. orthonormal right sigular vector set을 만든다.
    • 2.orthonormal left sigular vector set을 만든다.
    • 3. right sigular vector와 left sigualr vector를 엮으면서 linear mapping하에서 $v_i$의 orthogonality를 유지해야한다.
  • Eigenvalue Decomposition vs. Singular Value Decomposition

Singular Value Decomposition

SVD는 모든 matrix에 적용할 수 있기 때문에, ‘fundmental of linear algebra’라고 불려진다.

Theorem 4.22 (SVD Theorem)

$A \in R^{m \times n}$와 같은 matrix가 있을 때, A의 SVD는 아래와 같다. $A = U\Sigma V^T$

• $U \in R^{m \times m}$: orthogonal matrix, with column vectors $[u_1, \cdots, u_m]$

• $V \in R^{n \times n}$: orthogonal matrix, with column vectors $[v_1, \cdots, v_n]$

• $\Sigma \in R^{m \times n}$: $\Sigma_{ii} = \sigma_i \ge 0 \\ \Sigma_{ij} = 0 \text{ if } i \neq j$

$\sigma_i$는 singular value라고 하며, $u_i$는 left-sigular vector $v_i$는 right-singular vector라고 한다.

Geometric Intuitions for the SVD

위의 이미지를 3차원 데이터의 예시를 들어보면 아래와 같다.

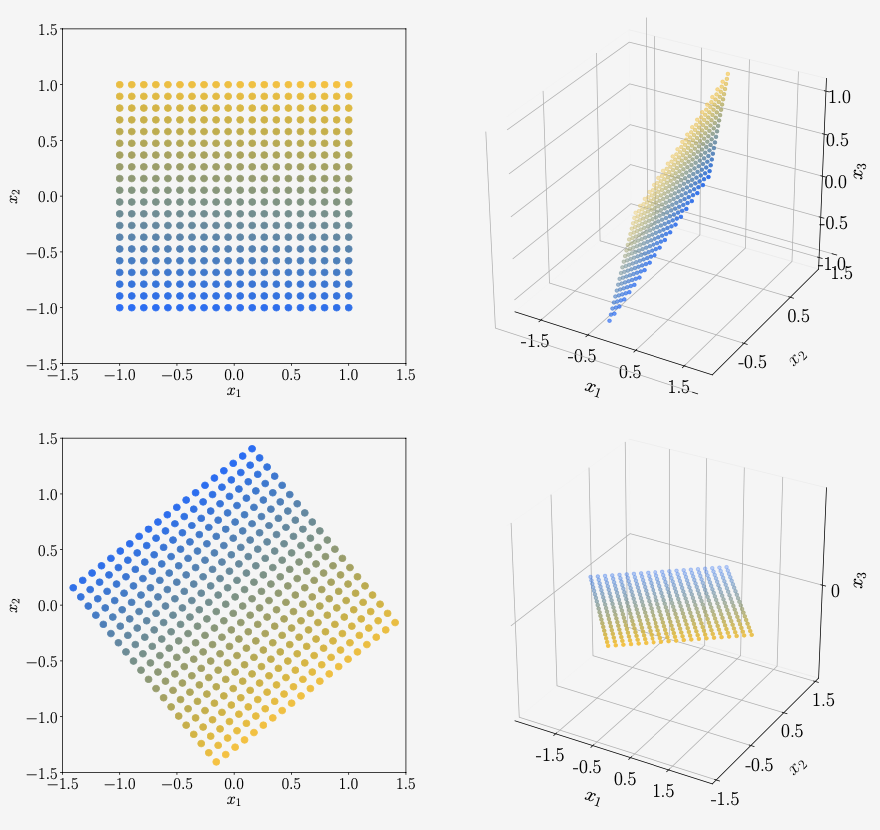
SVD는 linear mapping을 3개의 operation으로 나누어 본 것이다.

1. $V^T$로 basis change를 한다.

   $V$는 orthonormal matrix이기 때문에, $V^T = V^{-1}$이다.

2. $\Sigma$를 통해서 scaling을 한다.

3. $U$를 통해서 두 번째 basis change를 한다.

앞 서 살펴본 Eigendecomposition 에 대한 글에서는 basis를 원래 standard basis로 복원하는데, SVD는 그렇지 않다. 이는 rectagular matrix가 domain basis와 codomain basis가 다르기 때문이다.

Construction of the SVD

이번 섹션에서는 SVD가 존재하는 것을 증명해 볼 것이다. SVD는 eigendecomposition과 유사한 특성을 가진다.

Remark: symmetric positive definite matrix

SPD(symmetric positive definite matrix)의 eigendecomposition은 아래와 같다. $S = S^T =PDP^T$ SPD의 SVD는 아래와 같다. $S = U\Sigma V^T$ 만약 $U=P=V, D=\Sigma$로 정한다면, SPD의 SVD는 eigendecomposition과 같다.

증명의 큰 흐름은 아래와 같다.

1. orthonormal right sigular vector set을 만든다.
2. orthonormal left sigular vector set을 만든다.
3. right sigular vector와 left sigualr vector를 엮으면서 linear mapping하에서 $v_i$의 orthogonality를 유지해야한다.

1. orthonormal right sigular vector set을 만든다.

spectral theorem에 따르면, symmetrci matrix의 eigenvector는 orthonormal basis를 구성한다. 이것은 diagonalize가 가능하다는 것을 의미하기도 한다. 따라서, $A^TA$는 항상 아래와 같이 eigendecomosition이 될 수 있다. 이 때, $P$는 orthogonal eigenvector이며, $\lambda_i \ge 0$는 eigenvalue를 의미한다. $A^TA = PDP^T = P \begin{bmatrix} \lambda_1 & \cdots & 0\\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{bmatrix}P^T$ A의 SVD가 존재한다고 가정해보면, $A^TA = (U\Sigma V^T)^T(U\Sigma V^T) = V\Sigma^T U^TU\Sigma V^T = V \Sigma^T \Sigma V^T$

• U는 orthonormal matrix이기 때문에 $UU^T = I$이다.

조금 더 정리해보면, $A^TA = V \begin{bmatrix} \sigma_1^2 & \cdots & 0\\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_n^2\end{bmatrix}V^T$

위의 eigendecomposition의 식과 비교해보면, 아래와 같이 일치하는 것을 알 수 있다.

• $P=V$
• $\lambda_i = \sigma_i^2$

따라서, $AA^T$의 eigenvectors는 right sigular vectors를 구성한다.

2.orthonormal left sigular vector set을 만든다.

위와 유사한 과정을 통해서, left sigular vector sec을 만든다. $AA^T = SDS^T =(U\Sigma V^T)(U\Sigma V^T)^T = U\Sigma \Sigma^TU^T \\ = U \begin{bmatrix} \sigma_1^2 & \cdots & 0\\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_n^2\end{bmatrix} U^T$

• $V$는 orthonormal matrix이므로, $V^TV =I$이다.

• $S=U$
• $\lambda_i = \sigma_i^2$

$AA^T$와 $A^TA$가 같은 eigenvalue를 가진다는 것 eigenvalue의 특성으로 알 수 있다. 이를 통해서,$A^TA, AA^T$의 SVD의 $\Sigma$는 모두 동일해야한다. 즉, A의 SVD의 고유성이 확보되어야한다.

3. right sigular vector와 left sigualr vector를 엮으면서 linear mapping하에서 $v_i$의 orthogonality를 유지해야한다.

이제 앞에서 만들어둔, right singular vectors와 left singular vectors를 연결시킬 단계이다. 이를 위해서는, 아래와 같은 명제를 활용할 수 있다.

$v_i$가 orthogonal vector set이라면, $Av_i$도 orthogonal vector set이다. $(Av_i)^T (Av_j) = v_i^TA^TAv_j = 0$ 따라서, $[Av_1, \cdots, Av_r]$은 r dimensional subspace의 basis가 된다.

이를 활용해서 orthonormal vector $u_i$를 다음과 같이 $v_i$를 통해서 정의할 수 있다. $u_i = \frac{Av_i}{\rVert Av_i\rVert} = \frac{1}{\sqrt{\lambda_i}}Av_i = \frac{1}{\sigma_i}Av_i$ $AA^T$에서 $u_i$는 orthonormal 한 basis이므로 위와 같이 표현할 수 있다.

$Av_i = \sigma_iui$ $AV = \Sigma U$

위의 식의 의미는 orthonormal vector set을 linear transformation했을 때, 크기는 변할 수 있지만, 여전히 orthogonal한 vector set을 구성할 수 있다는 것을 보여준다.

Eigenvalue Decomposition vs. Singular Value Decomposition

square matrix $A \in R^{n \times n}$의 eigendecomposition과 svd를 고려해보자. $A = PDP^{-1} = U \Sigma V^T$

• eigendecomposition은 square matrix일때만 가능하지만, svd는 어떤 matrix형태든 가능하다.
• eigendecomposition의 P는 orthogonal하지 않다. 하지만, svd의 U, V는 orthonormal한 matrix이다.
  • 이러한 차이는 eigendecomposition은 rotation linear mapping을 표현하지 못하지만, svd는 할 수 있다.
• eigendecomposition과 svd는 모두 세개의 linear mapping으로 이루어져있다.
  1. Domain baisis로 변환하기
  2. new basis vector의 scaling
  3. Codomain basis로 변환하기. 이때, eigendecomposition은 domain과 codomain이 같지만, svd는 다르다.
• eigendecomposition은 첫 번째 basis change $P$와 마지막 basis change $P^{-1}$ 서로 역행렬 관계이지만, svd는 그렇지 않다.
• svd의 $\Sigma$는 real, non-negative가 보장되지만, eigendecomposition은 그렇지 않다.
• A의 left sigular vector은 $AA^T$의 eigenvector이다.
• A의 right sigular vector은 $A^TA$의 eigenvector이다.
• $AA^T, A^TA$의 eigenvalue의 square root는 A의 sigular value이다.
• symmetric matrix A의 eigendecomposition은 svd와 같다. (spectral theorem)

Example 4.14 (Finding Structure in Movie Ratings and Consumers)

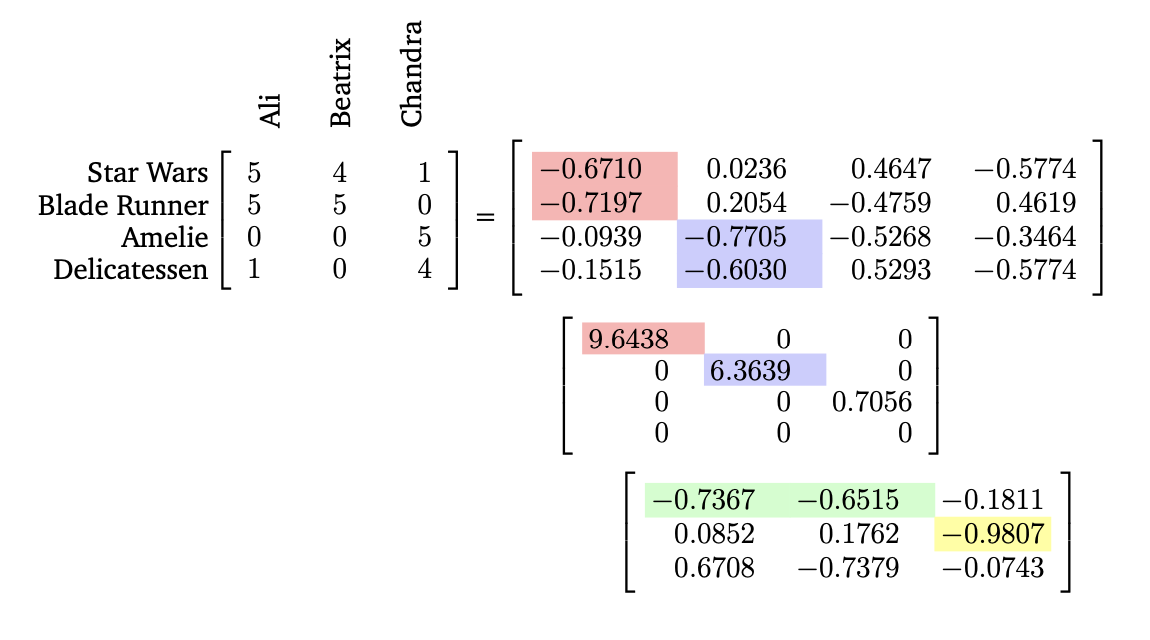
위에는 영화에 대한 선호도와 viewer에 대한 matrix A이다.

• Row: movie
• Col: viewer

A는 factorization을 해보면 어떤 viewer가 어떤 영화를 좋아하는지에 대한 정보를 얻을 수 있다. 그러기 위해서 몇 가지 가정을 하겠다.

• 모든 viewer은 같은 linear mapping으로 영화에 평점을 매겼다.
• 평가에는 error, noise가 없다.
• left sigular vector를 전형적인 영화, right sigular vector를 전형적인 viewer로 정의한다.

위의 가정을 바탕으로 조금 더 큰 가정을 할 수 있다. left sigular vector를 조합하게 되면, 한 viewer의 선호도를 알 수 있다. 마찬가지로, right sigular vector를 조합하면, 영화의 흥행력을 가늠해볼 수 있다.

그러므로, domain의 vector는 전형적인 viewer에 대한 vector 공간에서 해석될 수 있고, codomain은 전형적인 영화공간에서 해석될 수 있다.

Left sigular vector $u_1$의 첫번째, 두번째 성분의 절대값이 높은 것을 알 수 있다. 따라서, 두 영화에 영향을 많이 받는 vector라고 해석할 수 있다.

비슷하게, right sigular vector의 경우, 두 명의 viewer에 큰 값을 가지고 있다. 이 두명의 viewer는 공상영화에 큰 선호도를 가지고 있기 때문에 이 vector는 공상영화광이라고 해석할 수 있다.