이 논문에서는 epistemic uncertainty와 aleatoric uncertainty를 하나의 모델에서 측정하는 것을 제안하고 있습니다. (이전의 연구에서는 위의 uncertainty를 따로 분리하여 측정했다고 합니다.)

regression task에서 각각의 uncertainty에 대해서 알아보도록 하겠습니다.

Epistemic uncertainty

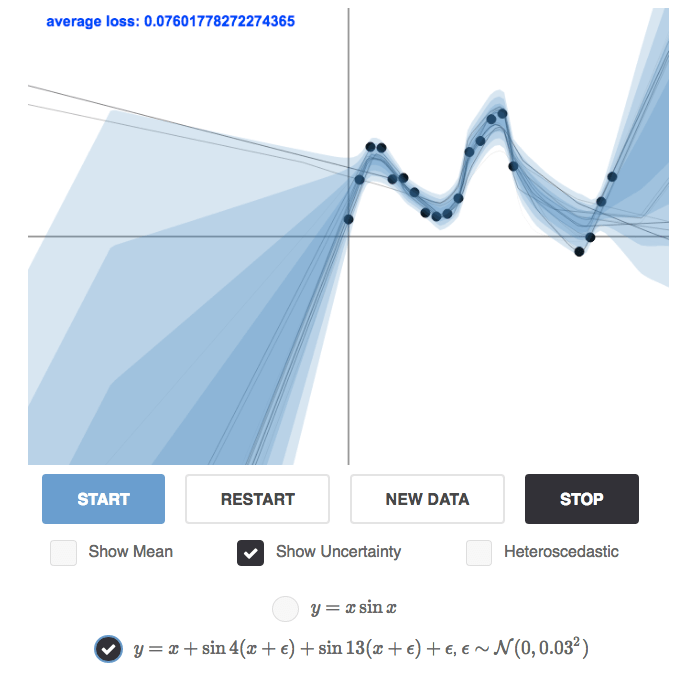
[Fig. 1]을 보면, 파란색 영역은 variance를 나타내며, observation(흑색 점)이 있는 data point에서는 낮은 unceratinty를 보이고 그렇지 않은 곳에서는 높은 uncertainty를 보인다. 만약 높은 variance를 보이는 영역에 data point가 더 있다면 uncertainty는 줄어들 것이다.

학습할 수 있는 데이터가 더 있다면 줄어들 수 있는 uncertainty를 ‘epistemic uncertainty’라고 한다.

epistemic uncertainty는 다음과 같은 모델에서 중요합니다.

  • Safety-ciritical applications: 자율주행자동차, 의료영상 등등
  • Small dataset: training 데이터가 부족한 domain

만약, Gaussian Process에 대해서 더 자세히 알고 싶다면 A Visual Exploration of Gaussian Process를 참고하길 바랍니다.

Aleatoric uncertainty

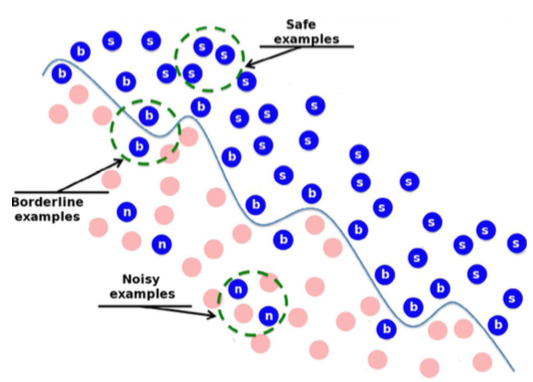
Aleatoric uncertainty는 data point 자체의 noisy를 의미한다. 이는 epistemic uncertainty와 다르게 더 많은 data point가 추가되어도 줄어들 수 없는 특성을 가지고 있다.

Heteroscedastic Aleatoric uncertainty

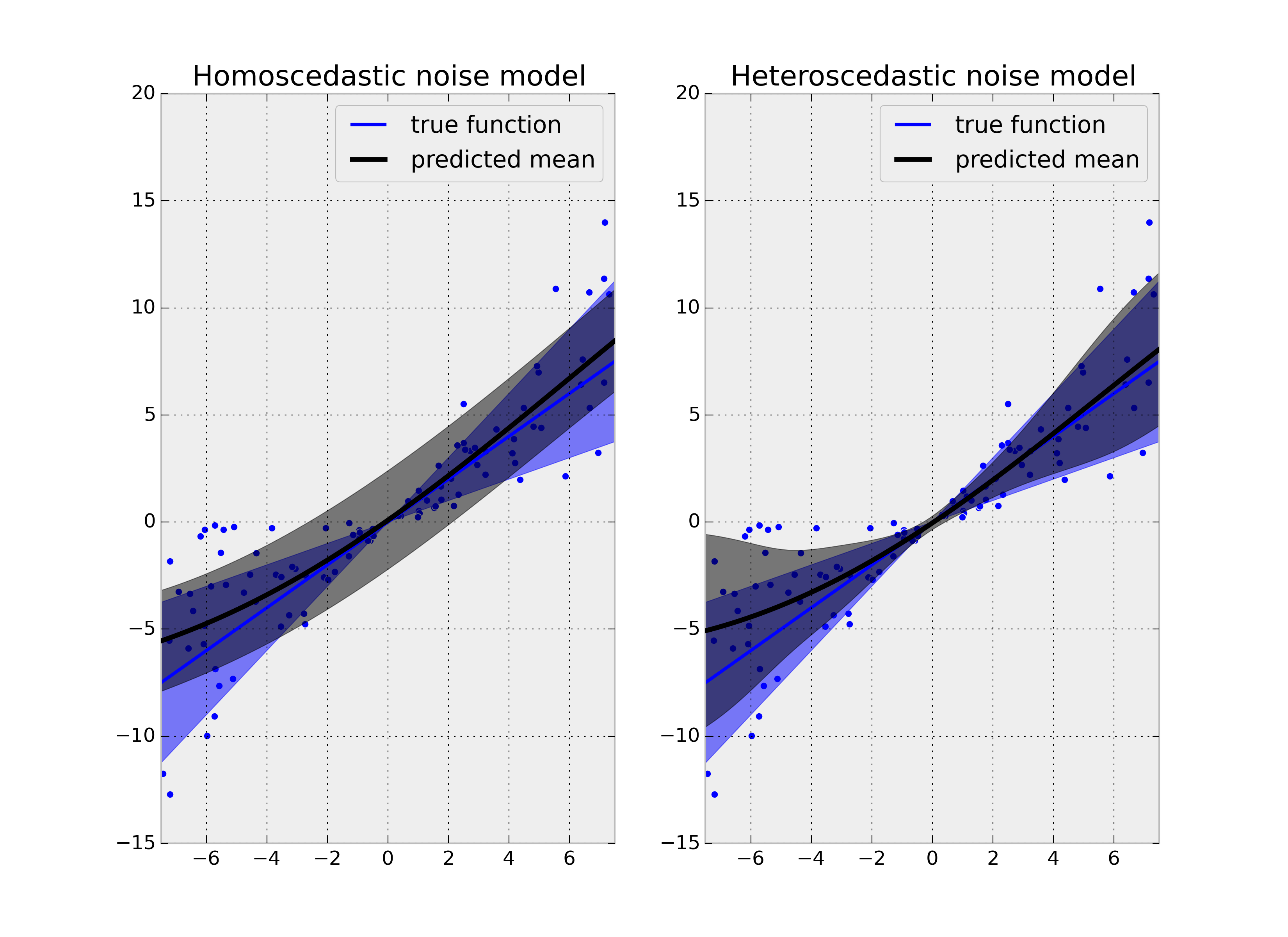
heteroscedastic noise model은 homescedastic noise model과 다르게 data point마다 다른 uncertainty를 가지고 있습니다. 이를 바탕으로 Aleatoric heteroscedastic uncetainty를 생각해보면, input data에 따라서 달라지는 uncertainty를 가진다고 생각하면 될 것 같습니다. 이 논문에서는 ‘Heteroscedastic Aleatoric uncertainty’를 가정하고 문제를 풀고 있습니다.

aleatoric uncertainty는 다음과 같은 모델에서 중요합니다.

  • Large data situations
  • Real-time applications: Monte-Carlo sampling없이 aleatoric model을 만들수 있기 때문입니다.

그럼 기존의 연구에서 어떻게 epistemic, aleatoric uncertainty를 접근했는지 살펴보겠습니다.

2.1 Epistemic Uncertainty in Bayesian Deep Learning

우선, epistemic uncertainty는 model의 weight에 prior distribution을 가정합니다. 그리고 data에 따라서 weight가 변하는 양상을 측정합니다.

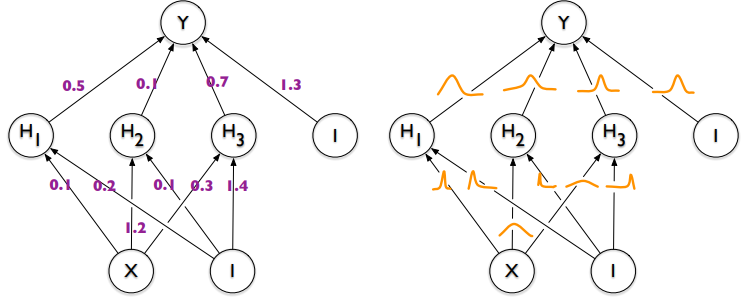
nueral network의 weight에 prior distribution을 설정하기 위해서 일반적으로 Gaussian prior distribution 을 사용합니다 ($W \sim \mathbf{N}(0, I) $) 그리고 이를 Bayesian neural network(BNN)라고 합니다.

Bayesian neural network는 deterministic한 weight paramters를 distribution으로 바꾸고 network의 weight를 직접적으로 바꾸는 것이 아니라, 모든 가능한 weight의 marginalization을 구하여 평균값을 구합니다

P(X)=∑yP(X,Y=y)=∑yP(X∣Y=y)×P(Y=y)P(X) = \sum_y P(X, Y =y) = \sum_y P(X|Y=y) \times P(Y=y)

Notation

  • $f^{W}(x)$: BNN의 random output

  • $X=[{x_1, x_2, \cdots, x_{n}}]$, $Y=[y_1, y_2, \cdots, y_{n}]$ : datasets

  • $p(y \mid f^{W}(x))$ : likelihood

  • $p(W \mid X, Y)$: posterior distribution

BNN에서 posterior distribution의 역할은 주어진 data에서 가장 적절한 parameter를 찾아주는 것입니다.. (주어진 데이터에서 해당 prameter가 얼마큼의 확률을 가지는지 나타내주는 값)

regression regression task에서 어떻게 적용되는지 아래의 수식을 보면 알 수 있습니다.

p(y∣fW(x))=N(fW(x),σ2)p(y|f^{W}(x)) = \mathbf{N}(f^{W}(x), \sigma^2)

수식을 보면, likelihood는 평균이 $f^{W}(x)$이고 observation noise가 $\sigma$인 Gaussian distribution을 따르는 것을 알 수 있습니다.

classification

p(y∣fW(x))=softmax(fW(x))p(y|f^{W}(x)) = \mathbf{softmax}(f^{W}(x))

classifiaction에서는 다른 방법을 취합니다. 일반적으로 위와 같이 output에 softmax를 취하는 형태로 likelihood를 측정합니다.

하지만, bayesian neural network는 수식적으로는 쉽게 해결할 수 있으나 inference과정에서 어려움이 있습니다. 이는 marginal probability $p(X \mid Y)$ 때문입니다. 이 probability는 아래와 같이 posterior p(W∣X,Y)p(W \mid X, Y)를 계산할 때 필요합니다.

p(W∣X,Y)=p(Y∣X,W)P(W)/p(X∣Y)p(W|X, Y) =p(Y|X, W)P(W)/p(X|Y)

marginal probability $p(X \mid Y)$가 가지는 의미를 한번 생각해보면, 이해하기 쉬울 것 같습니다.

먼저, MNIST dataset의 경우에는 label 1이 주어졌을 때 image1이 나올 확률을 구해야합니다. 이는 계산하기는 힘들지만 할 수는 있을 것 같습니다. 하지만, label = $[1, 3, 5, \cdots ]$가 주어졌을 때, $[image1, imga2, \cdots]$가 나올확률을 모두 계산하는 것은 비효율적이며 현실적으로 불가능합니다. (모든 data들의 경우의 수를 탐색해야합니다.)

위에서 posterior p(W∣X,Y)p(W \mid X, Y)를 계산하기 힘든 이유를 언급하였습니다. 이러한 문제를 해결하기 위해서 Variational inference라는 방법론을 사용합니다. 간단하게 생각하면, posterior p(W∣X,Y)p(W \mid X, Y) 대신에 Simple distribution qθ(W)q_{\theta}(W)을 가정하고 parameter $\theta$에 의해서 posterior p(W∣X,Y)p(W \mid X, Y)와 유사한 분포를 가지도록 조정합니다.

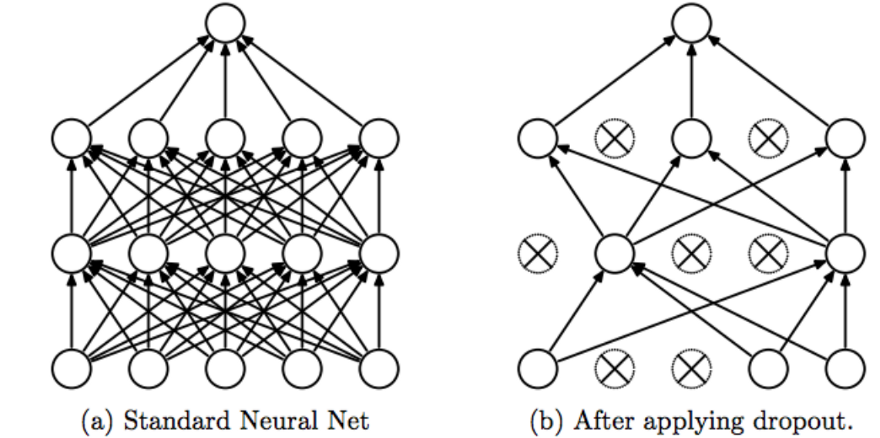
일반적으로 dropout은 overfitting을 막는 방법론으로 사용되고 있습니다. 하지만, dropout은 BNN과 유사한 inference를 할 수 있습니다. 이는 Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning 에서 확인할 수 있습니다. 간단하게 설명하면, 일반적으로 dropout은 train과정에서 적용하고 test과정에서는 제외하는데 반해서, bayesian inference를 하기 위해서 dropout을 train과 test과정에서 둘다 적용하여 사용합니다. 특히 test과정에서는 sampling을 하는데 dropout을 사용하고 있습니다. 이렇게 나온 sample을 바탕으로 inference를 진행합니다.

결론적으로, dropout은 아래와 같이 ‘variational bayesian approximation’으로 해석될 수 있습니다.

L(θ,p)=−1N∑_i=1Nlog⁡p(y_i∣fW^_i(xi))+1−p2N∥θ∥2\mathbf{L}(\theta, p) = -\frac{1}{N}\sum\_{i=1}^{N}\log{p(y\_{i}|f^{\hat{W}\_{i}}(x_{i}))} + \frac{1-p}{2N}\lVert \theta \rVert ^2

$N$은 data point를 의미하며, $p$는 dropout probability를 의미합니다. $\hat{W_i} \sim q_{\theta}(W)$의 samples weight를 가지고 있고 $\theta$를 이용하여 최적화합니다.

regression task에서는 위의 log likelihood를 아래처럼 변형할 수 있습니다.

−logp(yi∣fW^i(xi))∝12σ2∥yi−fW^i(xi))∥2+12log⁡θ2-log{p(y_{i}|f^{\hat{W}_{i}}(x_{i}))} \varpropto \frac{1}{2\sigma^2}\lVert y_i -f^{\hat{W}_{i}}(x_{i})) \rVert ^2 + \frac{1}{2}\log{\theta ^ 2}

여기서 $\theta$는 output에 대한 noise를 의미합니다. (data 자체의 noise가 아닙니다.)

위에서 언급했듯이 epistemic uncertainty 는 data point를 관측하면 감소되는 uncertainty입니다.

epistemic uncertainty를 이용하여, prediction uncertainty를 구할 수 있습니다. 아래는 classification task에서 Monte Carlo integration을 이용한 approximation입니다.

p(y=c∣x,X,Y)≈1T∑t=1TSoftmax(fW^i(xi))p(y=c|x,X,Y) \approx \frac{1}{T} \sum_{t=1}^{T}\mathbf{Softmax}(f^{\hat{W}_{i}}(x_{i}))

masked model weight $\hat{W_i} \sim q_{\theta}(W)$, $q_{\theta}(W)$은 dropout distiribution입니다..

probability vector $p$에 대한 uncertainty를 구할 때, entropy 개념을 이용하는데 이를 식으로 나타내면 아래와 같습니다.

H(p)=−∑c=1Cpclog⁡pcH(p) = -\sum_{c=1}^{C}p_c\log{p_c}

regression task의 경우 epistemic uncertainty는 predictive variance로 나타낼 수 있으며, 이는 아래의 식과 같습니다.

Var(y) ≈θ2+1T∑t=1TfW^i(xi)TfW^i(xi)−E(y)TE(y)\mathbf{Var}(y) \ \approx \theta^2 + \frac{1}{T}\sum_{t=1}^{T}f^{\hat{W}_{i}}(x_{i})^{T}f^{\hat{W}_{i}}(x_{i}) - \mathbf{E}(y) ^ {T}\mathbf{E}(y)

이 epistemic model은 $\mathbf{E}(y) \approx \frac{1}{T}\sum_{t=1}^{T}f^{\hat{W}{i}}(x{i}) $ predictive mean과 근사하는 방향으로 학습이 진행됩니다.($E(y)$ 는 predictive mean) 첫번째 term $\theta ^ 2$은 data 자체의 noise를 의미합니다. (aleatoric) 이는 뒷부분에서 자세히 다루겠습니다. 두번째 term은 predictive variance로 예측값에 대한 uncertainty를 나타냅니다. (epistemic)

참고로 aleatoric과 epistemic은 linear regression의 SSR, SSE의 개념과 유사합니다.

2. 2 Heteroscedastic Aleatoric Uncertainty

Aleatoric uncertainty는 model의 output에 distribution을 가정합니다. 그리고 이를 위해서 ‘observation noise parameter $\theta$’를 학습시킵니다.

위에서 언급했듯이, Homoscedastic regression은 모든 data point마다 동일한 observation constant noise $\sigma$를 가집니다. 반면에, Heteroscedastic model에서는 각 data point마다 서로 다른 observation noise를 가지고 있습니다. Non-Bayesian neural network에서는 대게 constance noise $\sigma$를 가정하거나, 무시하곤 합니다. 하지만, 아래 수식과 같이 data-dependent하게 학습시킨다면, data에 대한 fucntion의 형태로 학습될 수 있습니다.

LNN(θ)=1N∑i=1N12σ(xi)2∥yi−f(xi)∥2+12log⁡σ(xi)2\mathbf{L}_{NN}(\theta) = \frac{1}{N}\sum_{i=1}^{N}\frac{1}{2\sigma(x_i)^2}\rVert y_i - f(x_i) \rVert ^ 2 + \frac{1}{2}\log{\sigma(x_i)^2}

function의 형태로 학습시킨다는 것은 각 data point마다 변하는 uncertainty를 측정할 수 있다는 것을 의미합니다. 또한 epistemic uncertainty를 구하는 것과 다르게 variational inference 대신에 MAP inference를 사용합니다. - finding single value for the model parameters $\theta$

참고로 이런 방법은 epistemic uncertainty를 측정하지 못하는데, 위의 접근방법은 data자체의 uncertainty를 구하는 방법이기 때문입니다.

Combining Aleatoric and Epistemic Uncertainty in One Model

aleatoric uncertainty가 noisy data에 더 robust하게 만드는 과정으로 해석될 수 있다는 발견이 두 과정을 합칠 수 있게 하였습니다. (일종의 regularization term으로 해석)

3.1 Combining Heteroscedastic Aleatoric Uncertainty and Epistemic Uncertainty

Epistemic uncertainty와 aleatoric uncertainty를 함께 구하기 위해서 [2. 2 Heteroscedastic Aleatoric Uncertainty]을 bayesian NN에 적용하였습니다. 본 논문에서는 BNN의 posterior를 dropout variational distribution으로 근사하였습니다. (2.1 Epistemic Uncertainty in Bayesian Deep Learning의 dropout 참고)

위의 모델의 output은 다음과 같이 predictive mean, predictive variance를 가지게 됩니다.

[y^,σ^2]=fW^(X)[\hat{y}, \hat{\sigma}^2] = f^{\hat{W}}(X)

이때 model weight ${\hat{W}} \sim q(W)$로 근사합니다.

LBNN(θ)=1D∑i12σ^−2∥yi−yi^∥2+12log⁡σi^2\mathbf{L}_{BNN}(\theta) = \frac{1}{D}\sum_{i}\frac{1}{2} \hat{\sigma}^{-2}\rVert y_i - \hat{y_i} \rVert ^2 + \frac{1}{2}\log{\hat{\sigma_i}^2}

where

  • $D$는 image $x$에 해당하는 output pixel $y_i$의 개수이다. (pixel 단위의 objective)
  • $\hat{\sigma_i}^2$은 pixel $i$에 대한 $BNN$의 output(predictive variance)

위의 term은 두가지 성분으로 분리 될 수 있습니다.

  1. residual regression: $\frac{1}{D}\sum_{i}\frac{1}{2} \rVert y_i - \hat{y_i} \rVert ^2$
  2. uncertainty regularization: $\frac{1}{2}\log{\hat{\sigma_i}^2}$

실제로 위의 수식을 적용할 때는 아래와 같이 조금 변형된 수식으로 학습을 진행합니다. 이는 division-zero의 문제를 해결하기 위해서라고 합니다.

LBNN(θ)=1D∑i12exp(−log⁡σ^2)∥yi−yi^∥2+12log⁡σi^2\mathbf{L}_{BNN}(\theta) = \frac{1}{D}\sum_{i}\frac{1}{2} exp(-\log{\hat{\sigma}^2})\rVert y_i - \hat{y_i} \rVert ^2 + \frac{1}{2}\log{\hat{\sigma_i}^2}

아래는pixel y 에 대한 위의 모델의 predictive uncertainty를 근사하는 수식입니다.

Var(y)≈1T∑t=1Ty^t2−(1T∑t=1Ty^t)2+1T∑t=1Tσ^t2Var(y) \approx \frac{1}{T}\sum_{t=1}^{T}\hat{y}_t^2-(\frac{1}{T}\sum_{t=1}^{T}\hat{y}_t)^2 +\frac{1}{T}\sum_{t=1}^T\hat{\sigma}_t^2

with $[\hat{y}t, \hat{\sigma}_t]{t=1}^{T}$ a set of T smapled outputs: $[\hat{y}_t, \hat{\sigma}_t^2] = f^{\hat{W}_t}(X)$ for randomly masked weights ${\hat{W}_t} \sim q(W)$

위에서의 설명을 이해하셨다면, 첫번째 term은 epistemic을 두번째 term은 aleatoric을 의미한다는 것을 알 수 있습니다.

Experiment

Semantic Segmentation

table1.png

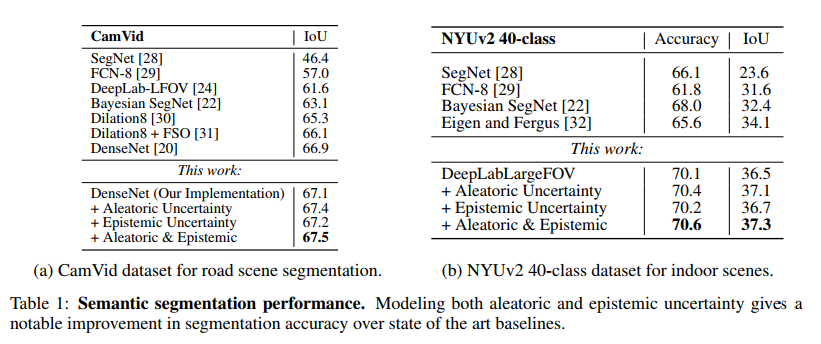
[Table 1 - a]Semantic segmentation task에서 실험한 결과 새로운 new state-of-the-art의 결과를 내었습니다. (IOU 67.5%)

[Table 1 - b] NYUv2는 위의 a의 dataset보다 더 어려운 task이다. (더 많은 class를 가지고 있다.) 결과는 아래의 이미지에서 확인할 수 있습니다.

Pixel-wise Depth Regression

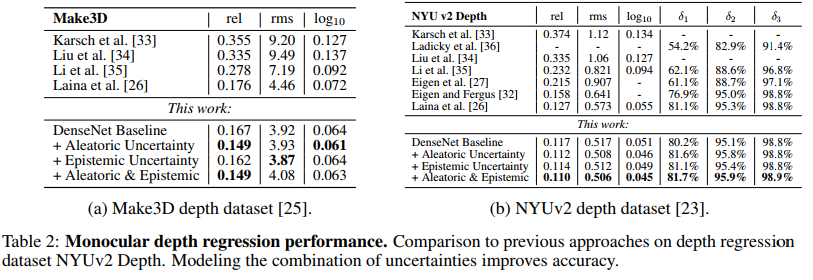
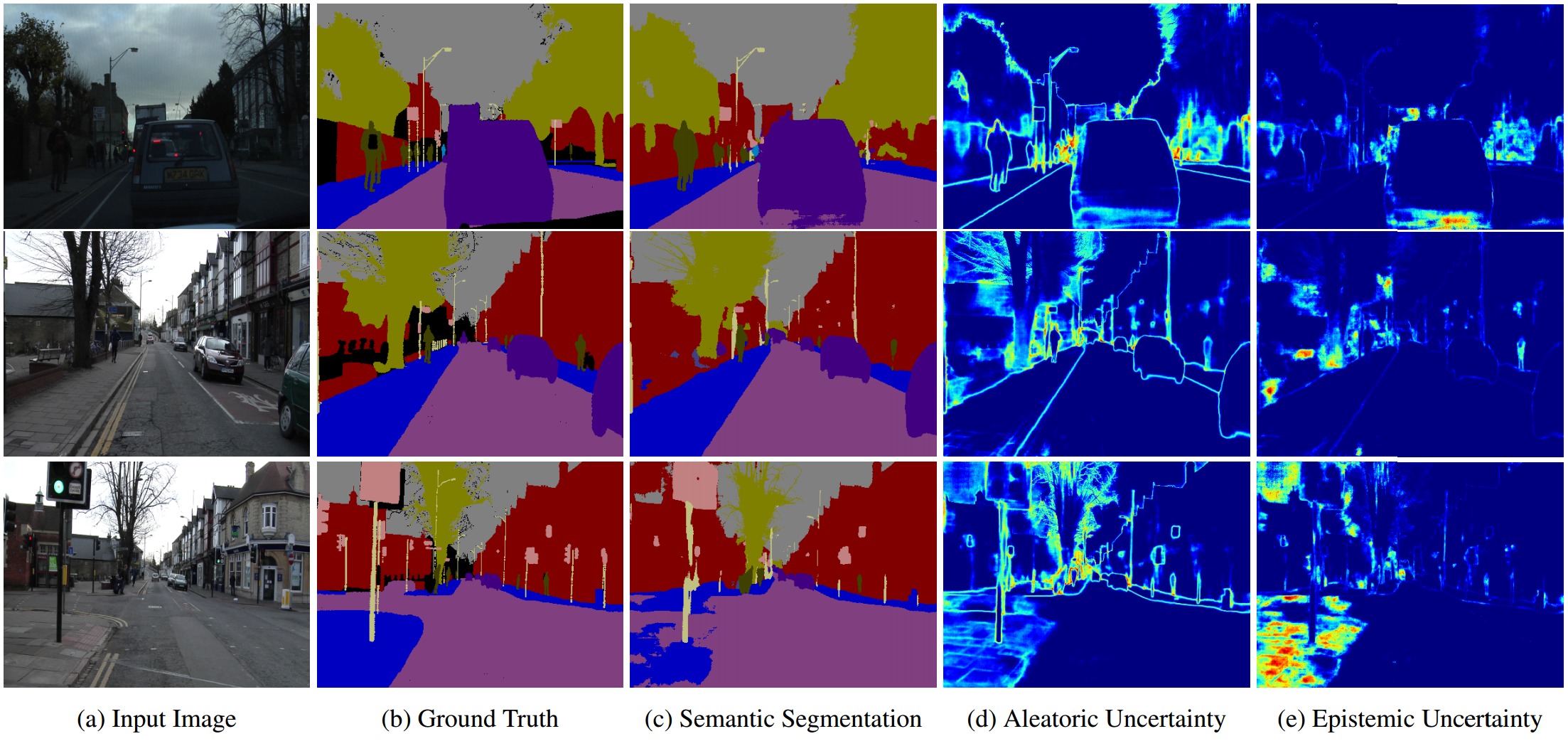
pixel의 depth regression task에서도 실험을 진행하였습니다. 실험결과 aleatoric uncertainty는 depth-regression task에서 많은 부분 기여할 수 있었습니다. 다음 이미지들을 보면 확인할 수 있습니다.

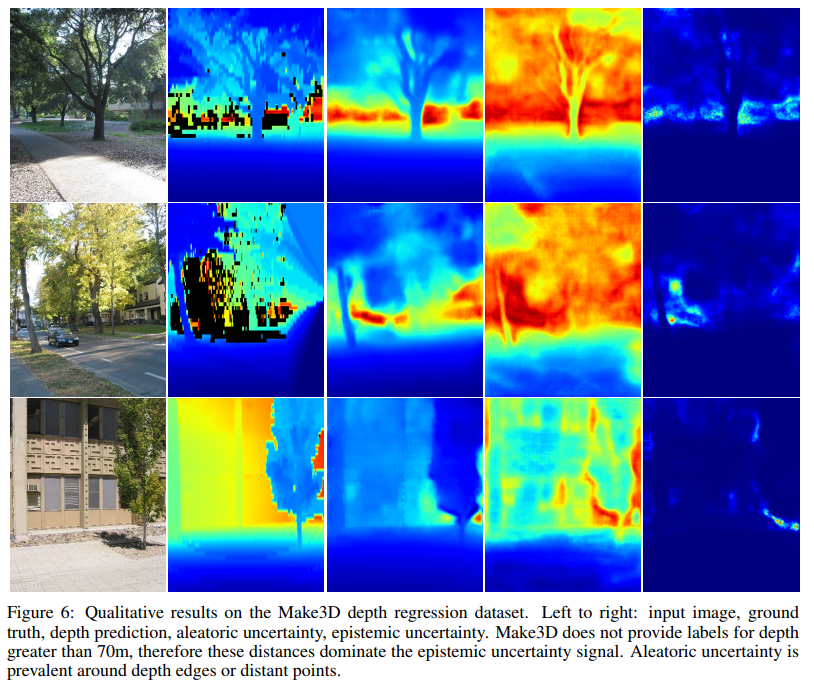
위의 이미지를 보면, aleatoric uncertainty는 depth가 깊을수록, 반사되는 표면을 가질수록, occlusion boundary일수록 높아지는 것을 확인할 수 있습니다. 이는 monocular depth algorithm들이 겪는 어려움들입니다. 반면에 epistemic uncertainty는 data가 부족한 점을 이용하여 이런 어려움들을 잡아냅니다. 예를 들어서 [Figure 5]에서 맨밑의 예를 보면, 사람이 있습니다. 이는 train data에 거의 없는 data로 epistemic uncertainty가 높아짐을 확인할 수 있습니다.

Analysis: What Do Aleatoric and Epistemic Uncertainties Capture?

5.1 Quality of Uncertainty Metric

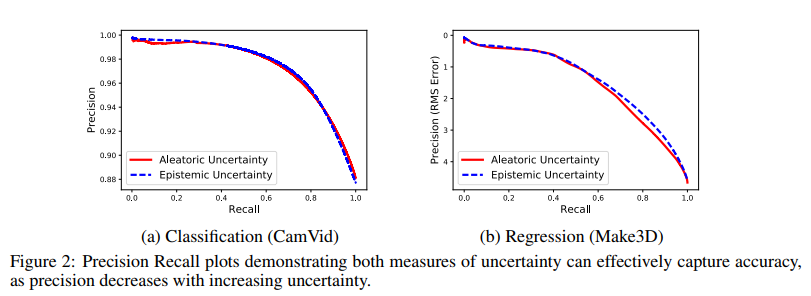
위의 이미지는 precision-recall 그래프이다. 해당 그래프는 threshhold보다 높은 uncertainty를 가지는 pixel을 제거할 때마다 model의 performance가 증가하는 것을 보여주고 있다. uncertainty가 높은 pixel을 제거하면 precision은 증가하지만, recall은 감소하게 된다.

  • precision: $\frac{tp}{tp + fp}$
  • recall: $\frac{tp}{tp + fn}$

첫번째로 uncertainty measurement가 accuracy와 상관관계가 있음을 보여주고 있다.

두번째로 epistemic uncertainty와 aleatoric uncertainty 그래프는 상당히 유사한 모양을 가지고 있다. 이것은 각 uncertainty가 다른 uncertainty와 비슷한 역할을 할 수 있다는 것을 의미한다.(다른 uncertainty가 없어도) 이는 하나의 uncertainty만 modeling하더라도 다른 uncertainty의 부족함을 채울려고 한다고 생각하면 된다.

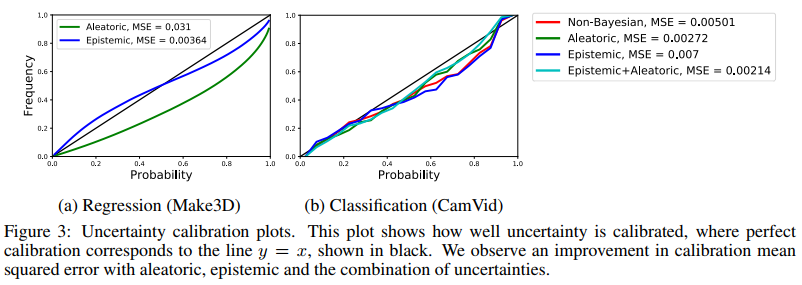
위의 이미지는 test set에 대한 calibration plot을 나타낸다. calibration plot이란 예측하는 확률값이 실제의 확률과 얼마나 유사한지 나타내는 역할을 한다. 예를 들어서, softmax value= 0.7이 실제로 70%의 확률로 나타나는지 확인하는 것이다. discret한 확률구간을 정의하고 각 확률구간에 대한 빈도를 측정한다. $y=x$ 그래프와 유사할수록 더 정확한 calibration이라고 할 수 있습니다.

5.2 Uncertainty with Distance from Training Data

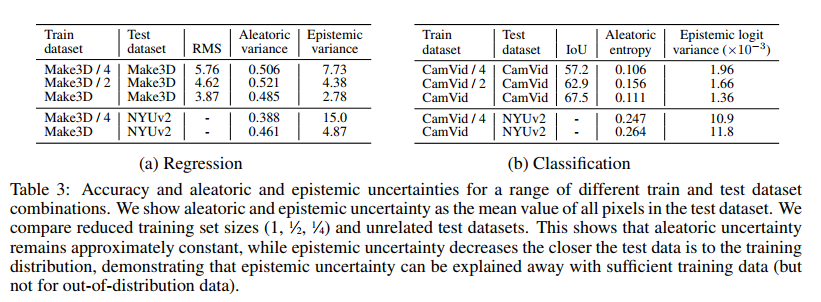
  • Aleatoric uncertainty는 더 많은 데이터가 있어도 설명할 수 없습니다.
  • Aleatoric uncertainty는 out-of-example(이상치)에 대해서 증가하지 않지만, epistemic은 증가합니다.

위의 실험결과는 epistemic uncertainty는 unseen data가 있는 상황에서 효과적이며 이는 safety-critical한 domain에서 효과적이라는 것을 보여줍니다.

5.3 Real-Time Application

aleatoric 자체는 모델을 계산할 때 많은계산량을 요구하지 않는반면, epistemic은 Monte-Calro sampling을 이용해야하기 때문에 이는 계산량이 많습니다. 따라서 real-time이 요구되는 application에서는 alatoric uncertainty만 적용하는 것도 방법이 될 수 있습니다.

현업에서 epistemic uncertainty를 적용하기에는 무리가 있는 상황입니다. 따라서 앞으로의 연구방향으로 real-time epistemic uncertainty을 deep learning에 적용하는 것은 중요한 이슈입니다.